Vai jūs zināt par ESP32 ADC pielāgošanu?: 29 soļi

2024 Autors: John Day | [email protected]. Pēdējoreiz modificēts: 2024-01-30 10:56

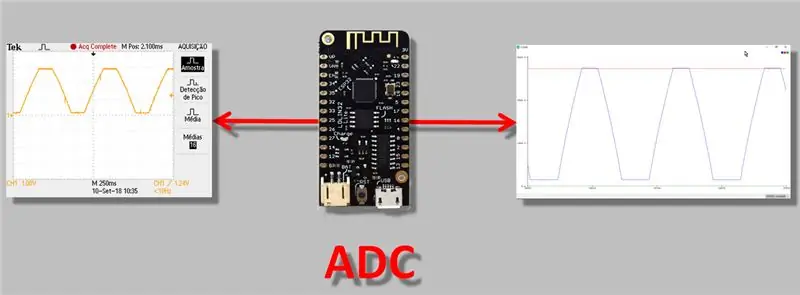
Šodien es runāšu par tehniskāku problēmu, taču, manuprāt, ikvienam, kas strādā ar ESP32, būtu jāzina: jautājums par ADC (analog-to-digital converter) lasīšanas pielāgošanu. Es uzskatu, ka tas ir svarīgi, jo, veicot "mērījumus", jo īpaši ar instrumentu, kuram ir analogā izeja, jums ir jābūt pilnīgi pārliecinātam, ka lasījums tiek veikts pareizi.

Tāpēc šodien videoklipā mēs veiksim mērījumus, izmantojot ESP32 "analogo-digitālo pārveidotāju", novērosim pārveidošanas neatbilstības un piemērosim ADC regulēšanas / kalibrēšanas metodi.

1. darbība: kas ir AD pārveidotājs?

AD pārveidotājs ir ķēde, kas spēj pārveidot analogo (nepārtraukto) daudzumu digitālās (diskrētās) vērtībās. Ko tas nozīmē? Tas nozīmē, ka, lai gan digitālās vērtības var pieņemt tikai atsevišķas vērtības, kas veidojas, apvienojot nulles un vienības, analogs daudzums var uzņemties jebkuru vērtību diapazonā. Piemēram, ja mēs izmērītu ideālas AA šūnas spriegumu, mēs varētu atrast jebkuru vērtību no 0V līdz 1,5V, jo tas ir analogs daudzums. Ideāla luktura izejas stāvoklim ir jāpieņem tikai divi stāvokļi (izslēgts vai ieslēgts), kas ir diskrēts lielums. Tā kā mikrokontrolleri strādā, izmantojot šo diskrēto loģiku, mums ir nepieciešama ķēde, kas spēj pārvērst analogo daudzumu digitālā (vai diskrētā).

2. darbība. Izmantotie resursi

• Viena Lolin32 Lite karte v1.0.0

• Tektronix TDS1001C osciloskops uzņemšanai

• Viens USB kabelis ESP32

• Hantek DSO4102C osciloskops kā signāla ģenerators

3. darbība: ESP32 ADC

Saskaņā ar Espressif datiem, ESP32 mikroshēmas izmērītajos rezultātos var radīt +/- 6% atšķirību no vienas mikroshēmas uz otru.

Turklāt reklāmguvumam NAV lineāras atbildes uz katru lasīšanai pieejamo diapazonu. Espressif nodrošina kalibrēšanas metodi un iesaka lietotājiem ieviest citas metodes, ja uzskata to par vajadzīgu, lai sasniegtu vēlamo precizitāti.

Mēs veiksim datu iegūšanu, un no tā mēs parādīsim ADC atbildes un piemēru, kā korekciju nolasīt, izmantojot matemātisku procesu.

Šo labojumu veikšanai ir vairāki (vienkāršāki vai sarežģītāki) veidi. Jūsu ziņā ir izvērtēt jūsu projektam piemērotāko.

Šeit parādītajam būs ilustratīvs mērķis un tas mēģinās pievērsties interesantiem punktiem, kurus var novērot korekciju laikā.

4. darbība. Izmantotā ķēde

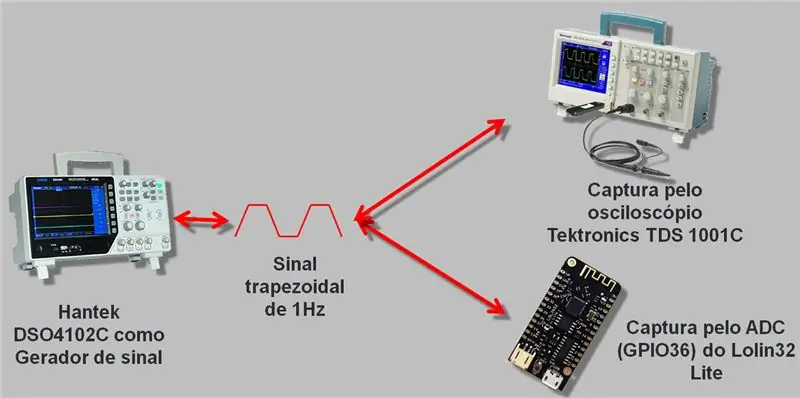
Es izmantoju osciloskopu ar signālu ģeneratoru, kas darbojas līdz 25 MHz, Hantek DSO4102C. Mēs ģenerējām vilni, ko nolasīja ESP A / D un osciloskops. Savāktie dati tika ierakstīti csv un izklājlapā, ko es atstāšu raksta beigās lejupielādei.

5. darbība: lietotā zīme

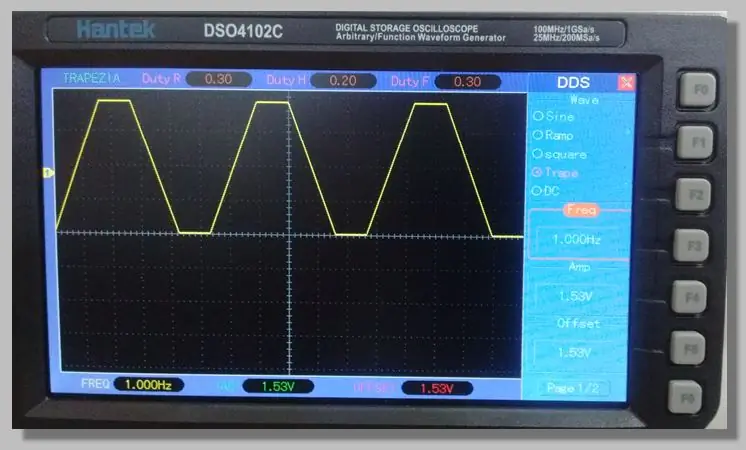
Mēs izvēlējāmies zemfrekvences trapecveida signālu, kas ļauj piekļūt rampām, kas darbojas visā pārveidošanas diapazonā. Tas ļauj uz šiem rampām uzņemt lielu skaitu paraugu.

6. darbība: Osciloskopa iegūtie dati

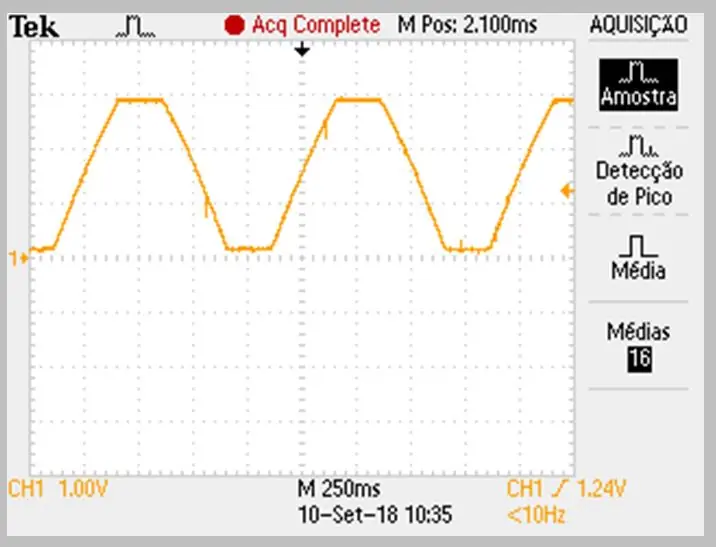
Uzņemšanas attēlu veica osciloskops. Dati tika saglabāti csv failā. Ņemiet vērā nelielo izliekumu uz signāla pieaugošajām un krītošajām rampām.

7. darbība: Osciloskopa iegūtie dati (csv fails programmā Excel)

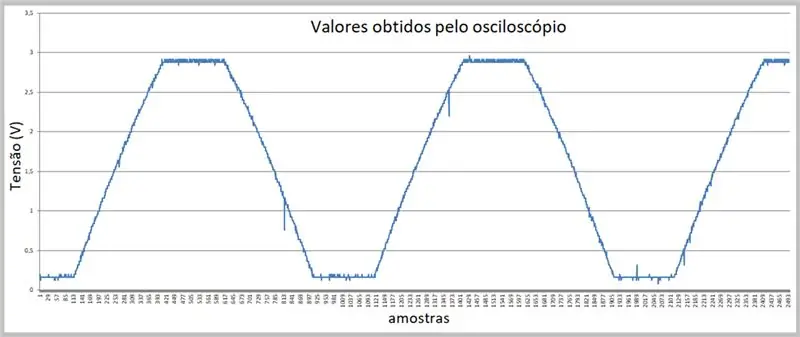
Šeit mums ir paraugi.

8. darbība: ADC iegūtie dati

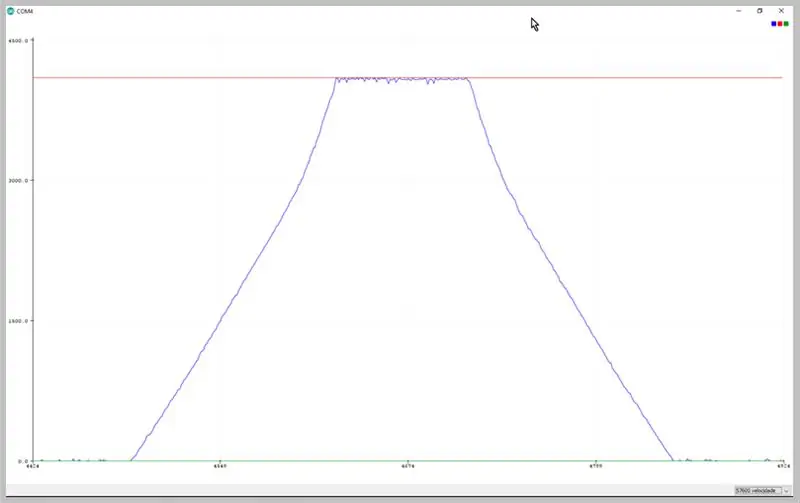
Mainot sērijas pārsūtīšanas ātrumu, mēs varam apskatīt ADC uztvertos datus. Ievērojiet trapecveida signāla deformāciju.

Dati, kas novēroti Arduino IDE sērijas ploterī

9. darbība. ADC iegūtie dati - Excel

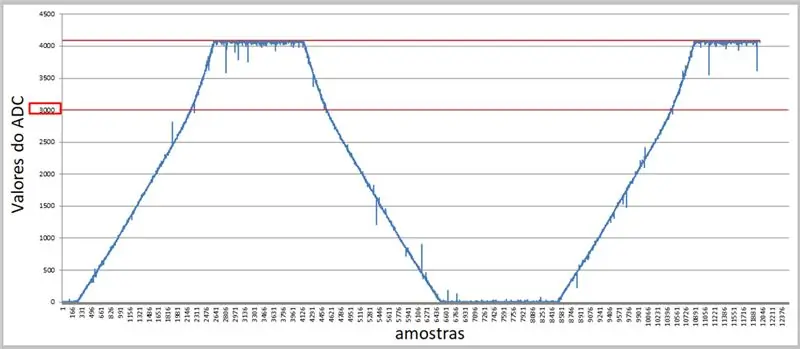
Izmantojot augstāku likmi un sērijveida termināli, mēs varam iegūt vērtības un izmantot tās programmā Excel salīdzinājumiem.

10. solis: kāpšanas rampu salīdzinājums

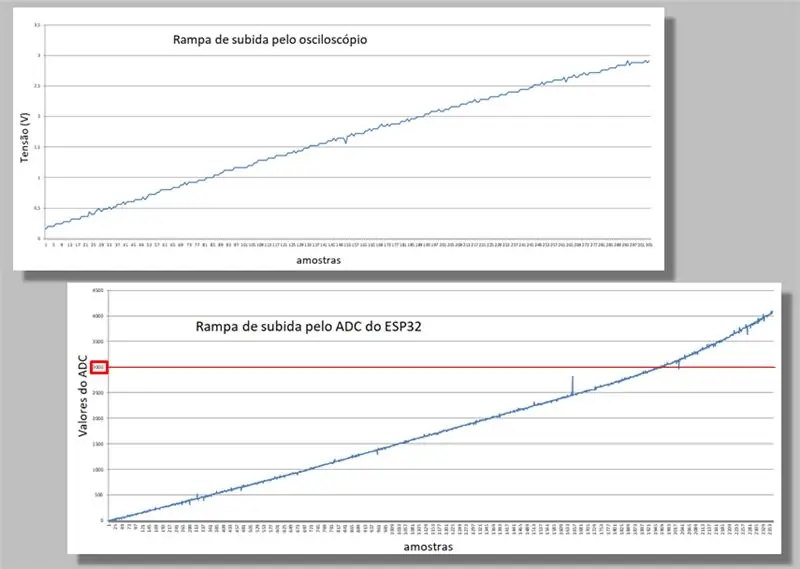
Mēs salīdzinām abu kāpņu divas kāpšanas rampas.

Ņemiet vērā izliekumu, kas rodas abās rampās.

Ņemiet vērā arī to, ka tajā pašā uzbrauktuvē mums ir daudz vairāk ESP32 paraugu nekā no osciloskopa.

11. solis: paraugu skaita pielīdzināšana

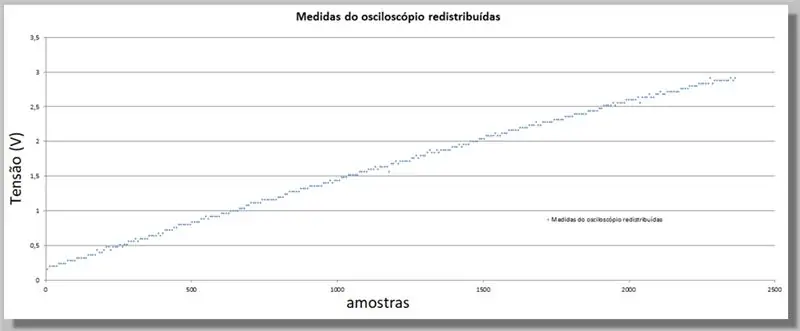
Tā kā ESP32 nodrošināja lielāku paraugu skaitu nekā osciloskops, mums šīs vērtības jāpielīdzina, jo tās kalpos kā indekss abu līkņu salīdzināšanai.

Šim nolūkam mēs veiksim tiešu salīdzinājumu.

Mums ir 305 paraugi osciloskopa rampai un 2365 paraugi ADC rampai.

Tā kā rampas ir vienāda diapazona, mēs varam teikt, ka mums ir aptuveni 7,75 ADC paraugi katram osciloskopam.

Reizinot katra osciloskopa parauga indeksu, ir tāda pati līkne, bet ar indeksiem, kas līdzvērtīgi ADC un pārdalītajiem datiem.

Lai aizpildītu trūkstošos datus par jaunajām pozīcijām, mēs izmantosim līkni, kas statistiski atbilst zināmajiem datiem.

12. solis: nepilnību aizpildīšana - tendenču līnija

Atlasot zināmos datus (zilos punktus), noklikšķinot un pēc tam noklikšķinot ar labo pogu, mēs izvēlamies "Pievienot tendences rindu …"

Parādītajā logā mēs izvēlamies polinomu veidu (pietiek ar 2. pasūtījumu).

Mēs pārbaudījām arī opcijas "Skatīt vienādojumu diagrammā" un "Rādīt diagrammā R kvadrāta vērtību".

Mēs noklikšķinām uz "Aizvērt".

13. solis: nepilnību aizpildīšana - 2. pakāpes polinomiskā līkne

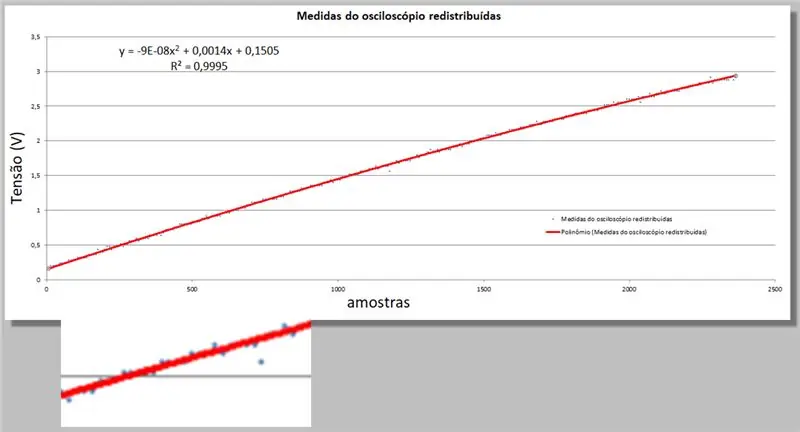
Excel sniedz mums divas jaunas informācijas; otrās kārtas vienādojums, kas vislabāk atbilst datiem, un R kvadrāta vienādojums, kas nosaka šo atbilstību.

Vienkārši atcerieties, ka, jo tuvāk 1, jo piemērotāks vienādojums.

Neiedziļināsimies iesaistītajā matemātikā, tikai izmantosim to kā rīku.

14. darbība: nepilnību aizpildīšana - funkcijas novērtēšana

Aizpildīsim izlases spraugas ar vienādojuma radītajiem datiem. Un tad salīdziniet tos pa punktiem.

y = -9E -08x2 + 0, 0014x + 0, 1505

R² = 0, 9999

Osciloskopa spriegums = -9E -08 * indekss2 + 0, 0014 * indekss + 0, 1505

15. solis: Osciloskopa sprieguma pārveidošana par līdzvērtīgu vērtību, lai to salīdzinātu ar ADC

Izmantosim šo iespēju, lai arī osciloskopa sprieguma vērtību pārveidotu par līdzvērtīgu ADC vērtību.

Tā kā augstākā vērtība, kas iegūta ESP32 ADP, bija 4095, kas ir līdzvērtīga 2,958 V rādījumam par to pašu indeksu, mēs varam teikt, ka:

Katrs volts osciloskopa mērījumos ir aptuveni 1384,4 AD vienības. Tāpēc mēs varam reizināt visus osciloskopa mērījumus ar šo vērtību.

16. solis: divu iegūto rampu salīdzināšana

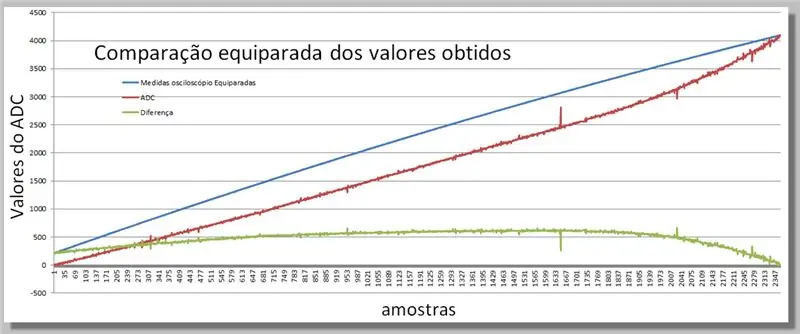
Vizualizējot abos lasījumos iegūtās atšķirības.

17. darbība: ADC lasīšanas atšķirības (ERROR) uzvedība

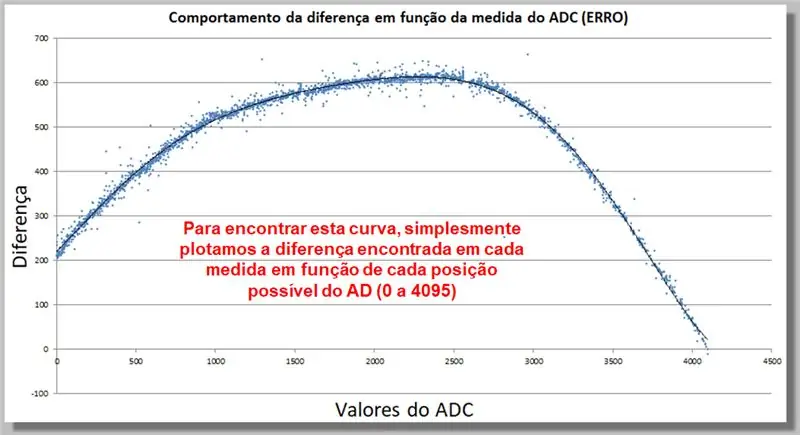
Tālāk redzamā līkne parāda, kā ADC rādījuma atšķirība darbojas kā mērījuma funkcija. Šī datu apkopošana ļaus mums atrast korekcijas funkciju.

Lai atrastu šo līkni, mēs vienkārši uzzīmējam katrā mērījumā atrasto atšķirību kā funkciju no katras iespējamās AD pozīcijas (no 0 līdz 4095).

18. solis: ADC lasīšanas atšķirību uzvedība - korekcijas funkcijas atrašana

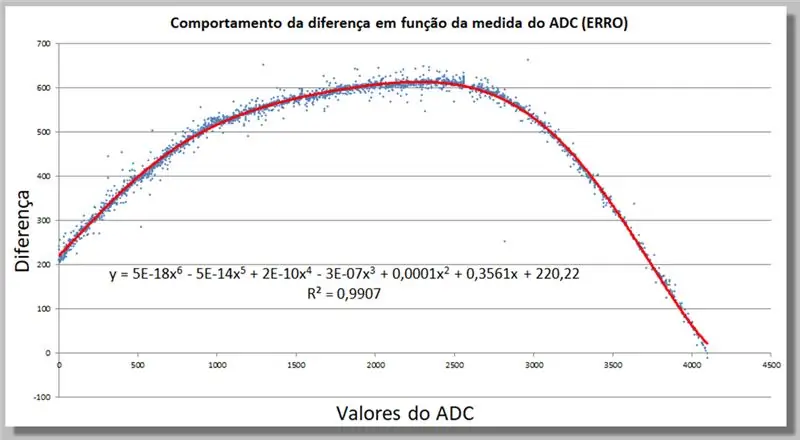
Mēs programmā Excel varam noteikt korekcijas funkciju, pievienojot augstākas pakāpes tendences līniju, līdz tā pietiekami atbilst mūsu datiem.

19. darbība: citas programmatūras izmantošana

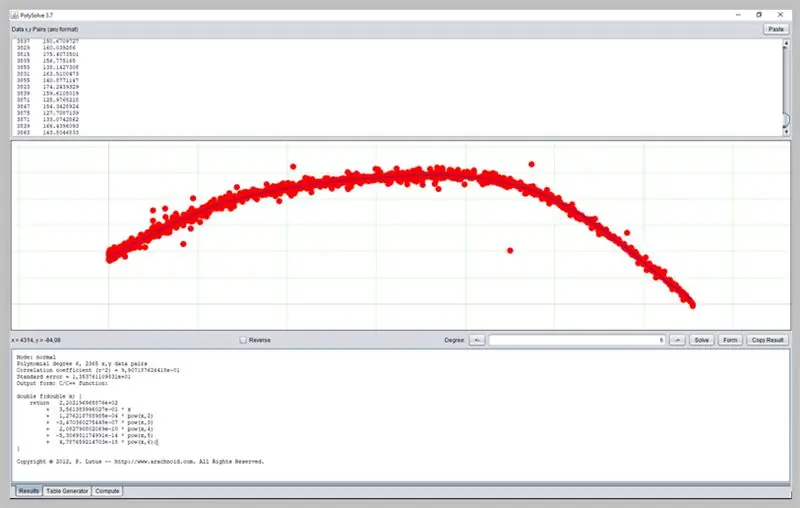
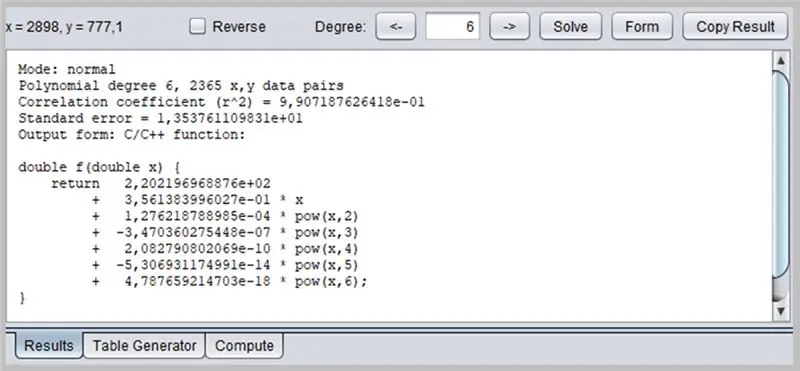
Cita interesanta programmatūra līkņu noteikšanai ir PolySolve, kuru var izmantot tieši saitē: https://arachnoid.com/polysolve/ vai lejupielādēt kā Java lietojumprogrammu.

Tas ļauj piemērot augstākas pakāpes polinomu regresijas un piegādāt formatēto funkciju, kā arī citas funkcijas.

Lai to izmantotu, vienkārši ievadiet datus pirmajā tekstlodziņā. Datiem jāatbilst secībai X, Y, atdalot tos ar komatu vai cilni. Esiet piesardzīgs, pareizi izmantojot punktu kā komatu.

Ja ievadītie dati ir pareizi formatēti, nākamajā lodziņā parādīsies diagramma.

Lūk, kā gāja mūsu ADC kļūdu līkne.

Šajā logā tiks parādīts regresijas rezultāts, ieskaitot funkciju atbilstības datus, kuru izvadi savukārt var tikt formatēti vairākos veidos: kā C / C ++ funkcija, koeficientu saraksts, Java rakstīta funkcija utt.

Piezīme: pievērsiet uzmanību decimāldaļām

20. darbība. Konstantes un iestatīšana ()

Šeit es norādīšu GPIO, ko izmanto analogai uztveršanai. Es inicializēju seriālo portu, kā arī tapu, kas noteikta analogai uztveršanai.

const int pin_leitura = 36; // GPIO usado para captura analógica void setup () {Serial.begin (1000000); // Iniciciando a porta serial somente para debug pinMode (pin_leitura, INPUT); // Pino utilizado para captura analógica}

21. darbība: cilpa () un korekcijas funkcija

Mēs uztveram regulēto spriegumu un drukājam vērtības ar pareizām korekcijām vai bez tām.

void loop () {int valor_analogico = analogRead (pin_leitura); // realiza a captura da tensão ajustada // Serial.print(valor_analogico + f (valor_analogico)); // imprime os valores para debug (COM CORREÇÃO) Serial.print (valor_analogico); // imprimime os valores para debug (SEM CORREÇÃO) Serial.print (","); Serial.print (4095); // cria uma linha para marcar o valor máximo de 4095 Serial.print (","); Sērijas.println (0); // cria uma linha para marcar o valor mínimo de 0}

Ievērojiet 12. rindā, ka mums ir iespēja drukāt datus, pievienojot starpības funkciju f (analog_value).

22. darbība: PolySolve Correction funkcijas izmantošana

Šeit mēs izmantojam funkciju PolySolve Arduino IDE iekšpusē.

/* Režīms: normāls polinomu grāds 6, 2365 x, y datu pāri Korelācijas koeficients (r^2) = 9, 907187626418e-01 Standarta kļūda = 1, 353761109831e+01 Izvades forma: C/C ++ funkcija: Autortiesības © 2012, P. Lutus - https://www.arachnoid.com. Visas tiesības aizsargātas. */ double f (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e- 10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

Atzīmējiet komatu pa punktam kā decimāldaļu atdalītāju.

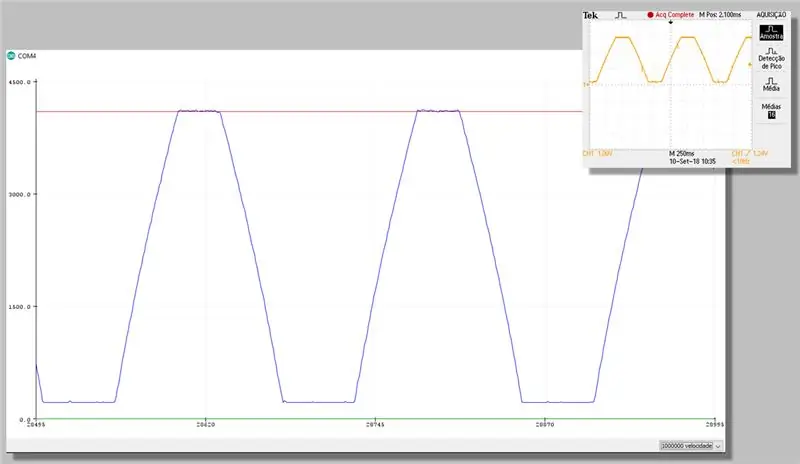
23. darbība. Uzņemiet ar labojumu - ploteru sērija

24. darbība: skaitļošanas izmaksas

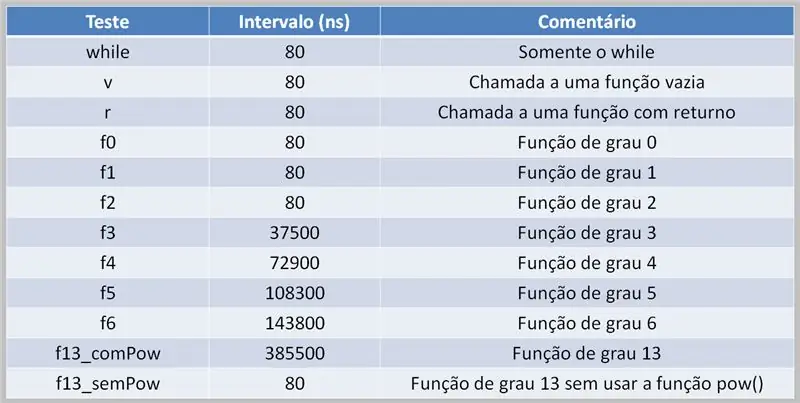
Lai veiktu polinomu aprēķinus, ir nepieciešams, lai procesors tiktu galā ar šo uzdevumu. Tas var izraisīt izpildes aizkavēšanos atkarībā no avota koda un pieejamās skaitļošanas jaudas.

Šeit mēs redzam testa rezultātu tabulu, izmantojot daudzpakāpju polinomus. Ievērojiet atšķirību starp laiku, kad tika izmantota funkcija pow (), un kad tā nebija.

25. darbība. Pārbaudes kods - iestatīšana () un cilpas sākšana ()

Šeit mums ir mūsu testā izmantotais kods.

void setup () {Serial.begin (1000000); // Iniciando a porta serial somente para debug} void loop () {float valor_analogico = 500.0; // um valor arbtrario float quantidade = 10000,0; // quantidade de chamadas float contador = 0.0; // contador de chamadas

26. darbība. Pārbaudes kods - cilpa () un apstrāde

Es izmantoju funkciju micros (), lai iegūtu vērtību mikrosekundēs.

// ============= inicia o o processo float agora = micros (); // marca o instante inicial while (contador <quantidade) {// v (valor_analogico); // função vazia // r (valor_analogico); // função com retorno // f0 (valor_analogico); // grau 0 // f1 (valor_analogico); // grau 1 // f2 (valor_analogico); // grau 2 // f3 (valor_analogico); // grau 3 // f4 (valor_analogico); // grau 4 // f5 (valor_analogico); // grau 5 // f6 (valor_analogico); // grau 6 // f13_semPow (valor_analogico); // grau 13º SEM a função POW // f13_comPow (valor_analogico); // grau 13º COM a função POW contador ++; } agora = (micros () - agora) / quantidade; // determina o intervalo que se passou para cada iteração // ============= finaliza o processo

27. darbība: pārbaudes kods - cilpa () - rezultāti

Salīdzinājumam mēs drukājam vērtību, kas atgriezta no 13. pakāpes funkcijas ar un bez POW, kā arī apstrādes intervālu.

// imprime o valor retornado da função de grau 13 com e sem POW para comparação Serial.print (f13_semPow (valor_analogico)); // grau 13º SEM a função POW Serial.print (" -"); Serial.print (f13_comPow (valor_analogico)); // grau 13º COM a função POW Serial.print (" -"); // imprime o intervalo do processamento Serial.println (agora, 6); }

28. darbība. Pārbaudes kods - izmantotās funkcijas

0 un 1 pakāpes tukšas funkcijas (tikai ar atgriešanos).

// FUNÇÃO VAZIAdouble v (double x) {} // FUNÇÃO SOMENTE COM RETORNO double r (double x) {return x; } // FUNÇÃO DE GRAU 0 double f0 (double x) {return 2.202196968876e+02; } // FUNÇÃO DE GRAU 1 double f1 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x; }

2., 3. un 4. pakāpes funkcijas.

// FUNÇÃO DE GRAU 2double f2 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2); } // FUNÇÃO DE GRAU 3 double f3 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3)); } // FUNÇÃO DE GRAU 4 double f4 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3)) + 2.082790802069e-10 * pow (x, 4); }

5. un 6. pakāpes funkcijas.

// FUNÇÃO DE GRAU 5double f5 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5); } // FUNÇÃO DE GRAU 6 double f6 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3)) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

13. pakāpes funkcija, izmantojot POW.

// FUNÇÃO DE GRAU 13 USANDO O POWdouble f13_comPow (double x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * pow (x, 2) + -3, 968558178426e-06 * pow (x, 3) + 1, 047910519933e-08 * pow (x, 4) + -1, 479271312313e-11 * pow (x, 5) + 1, 220894795714e-14 * pow (x, 6) + -6, 136200785076e-18 * pow (x, 7) + 1, 910015248179e-21 * pow (x, 8) + -3, 566607830903e-25 * pow (x, 9) + 5, 000280815521e-30 * pow (x, 10) + 3, 434515045670e-32 * pow (x, 11) + -1, 407635444704e-35 * pow (x, 12) + 9, 871816383223e-40 * pow (x, 13); }

13. pakāpes funkcija, neizmantojot POW.

// FUNÇÃO DE GRAU SEM USAR O POWdouble f13_semPow (double x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * x * x + -3, 968558178426e-06 * x * x * x + 1, 047910519933e-08 * x * x * x * x + -1, 479271312313e-11 * x * x * x * x * x + 1, 220894795714e-14 * x * x * x * x * x * x + -6, 136200785076e-18 * x * x * x * x * x * x * x + 1, 910015248179e-21 * x * x * x * x * x * x * x * x + -3, 566607830903e- 25 * x * x * x * x * x * x * x * x * x + 5, 000280815521e-30 * x * x * x * x * x * x * x * x * x * x + 3, 434515045670e- 32 * x * x * x * x * x * x * x * x * x * x * x + -1, 407635444704e -35 * x * x * x * x * x * x * x * x * x * x * x * x + 9, 871816383223e-40 * x * x * x * x * x * x * x * x * x * x * x * x * x; }

29. darbība: faili

Lejupielādējiet failus:

PDF

ES NĒ

Izklājlapa