Blink Caos: Kartes logotips Para Random Blink: 5 soļi

2024 Autors: John Day | [email protected]. Pēdējoreiz modificēts: 2024-01-30 10:52

Este ir un instructable para un generador de aleatoriedad, utilizando un mapa logístico, que ahora explico que es. Con el mapa logístico, se enciende y apaga un led de forma aleatoria. Este puede servir simplemente de ejemplo de como a través del caos se generan comportamientos aparentemente aleatorios. No se si es lo más práctico, pero es entretenido

1. darbība: materiāli

Ocupamos:

1. Arduino UNO
2. Maizes dēlis
3. Kabeļi
4. Vadīja
5. 10 kΩ jaudas jauda

2. solis: Koneksiones

El led lo conectamos al pin 13 (pata larga) y a tierra (pata corta). Como estamos en el pin 13, no ocupamos una resistencia.

El potenciciómetro, lo conectamos a "5V" la pata izquierda, a "GND" la pata derecha, y la del centro a A0.

Tā arī es!

3. solis: Logistikas karte

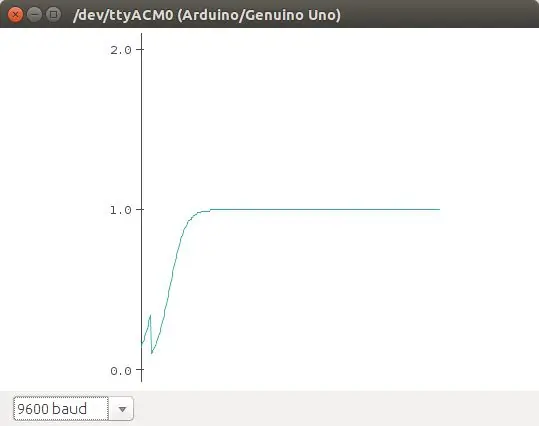
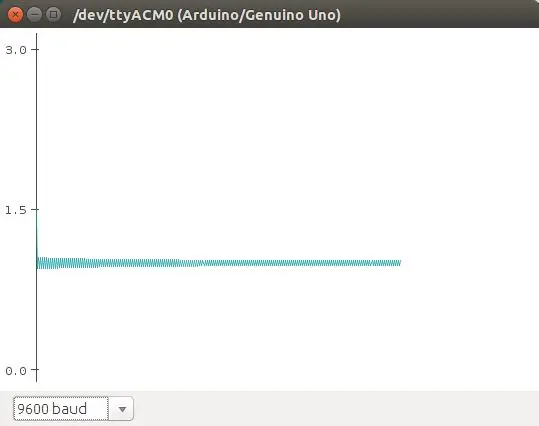
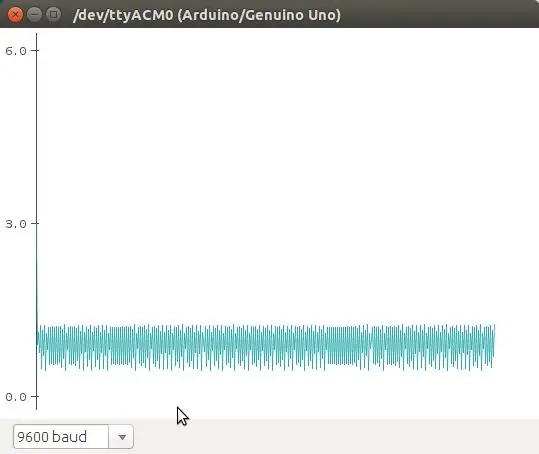
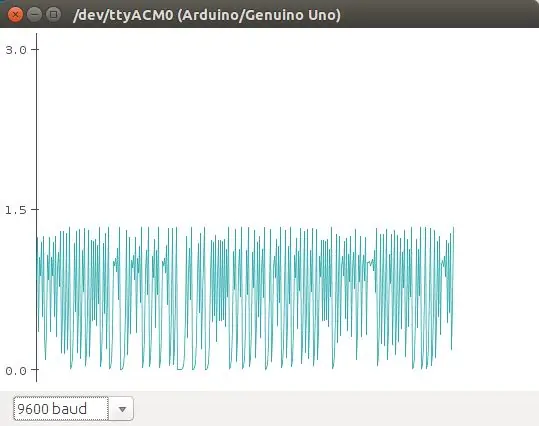
El mapa logístico es una ecuación que apraksta el crecimiento logístico de una población. Es una ecuación discreta en tiempo que va paso a paso, en tiempos discretos, re-calculando el tamaño de la población. Esta ecuación muestra como comportamiento caótico puede emerger de una ecuación tan simple. Fue popularizada por Robert May en 1976. La ecuación:

n (t+1) = r * n (t) * (1 - n), aprakstīt a la población en t+1, como una función de la población en t, multiplicado por su potencial biótico (como se reproducēt), y un efecto denso -dependiente que se ieviest en el término (1 - n). Esta es la versión normalizada de la ecuación. Básicamente, debido al termino (1 - n), la población crece si n> 1, y decce n <1.

En este ejemplo vamos a utilizar como punto crítico cuando la población n> 1, que se encienda el led. El potciómetro se utiliza para cambiar los valores de r en la ecuación.

En las fotos se muestran algunos de los comportamientos que se obtienen de esa ecuación (graficados con el plotter de Arduino).

Pueden leer más sobre el mapa logístico en wikipedia

4. solis: Código

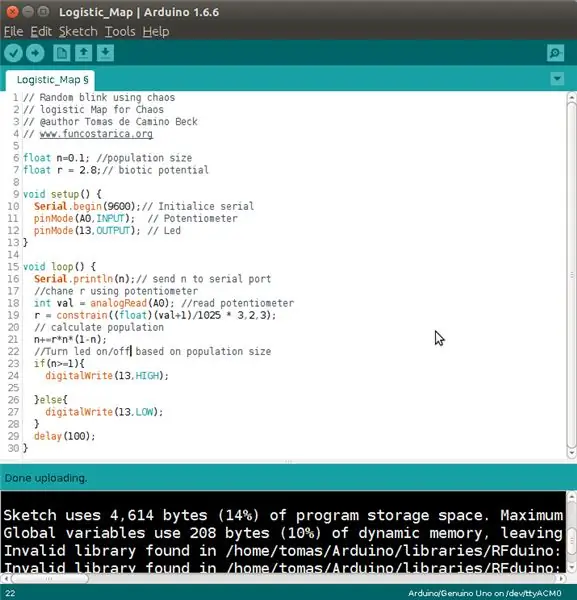
En el código lo importante está en el cuerpo princip del del program (loop), que es el que se utiliza para iterar sobre la ecuación del mapa logístico. En las líneas 6 y 7 se definen dos variables globales n para el tamaño de población y r para potencial biótico.

En la línea 18 se lee el potenciómetro, y en la 19, se convierte, primero a una escala de valor entre 0 y 1, y luego a un valor entre 0 y 3, aunque a eso se le aplica "constrain", para limitar los tipos de comportamiento que quiero con el potencimetro (hay varias maneras de hacerlo y esta probablemente no es la mejor)

De las líneas 23 a la 28 simplemente se lemt cuando prender el led.

Pielāgojiet el código para que lo puedan.

5. darbība: Funcionando

Como ven al mover el potencimetro pasamos de oscilaciones periódicas, es decir un blink intermitente con ciclos regulares, and uno caótico.

Esto se puede usar para tener un generador de ciclos de diferentes períodos, hasta llegar al caos.