Rekursīvi apkopojot masīvu Java: 9 soļi

2024 Autors: John Day | [email protected]. Pēdējoreiz modificēts: 2024-01-30 10:53

Rekursija ir ļoti noderīga un laikietilpīga procedūra, kas var ātri atrisināt problēmu ar ļoti mazu kodu. Rekursija ietver jūsu izveidoto metodi, kas saīsina sākotnējo problēmu.

Šajā piemērā mēs apkoposim 10 veselu skaitļu masīvu, bet izmērs var būt jebkura garuma.

Piegādes

Jums vajadzētu zināt Java pamata sintaksi un izmantot savu IDE vai teksta redaktoru, lai rakstītu kodu šim uzdevumam.

1. darbība: iestatiet savu galveno metodi

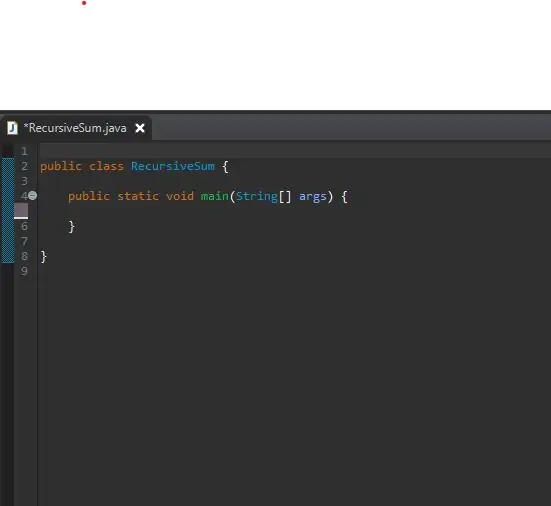
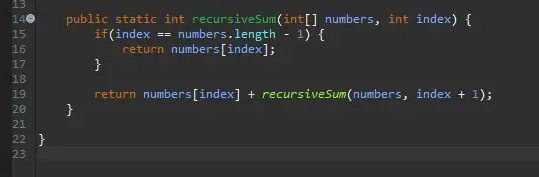
Lai sāktu, iestatiet savu galveno metodi jaunizveidotā klasē. Es savu klasi esmu nosaucis par RecursiveSum. Šeit jūs izveidosit veselu skaitļu masīvu un izsauksit savu rekursīvo metodi.

2. darbība: izveidojiet rekursīvās metodes galveni

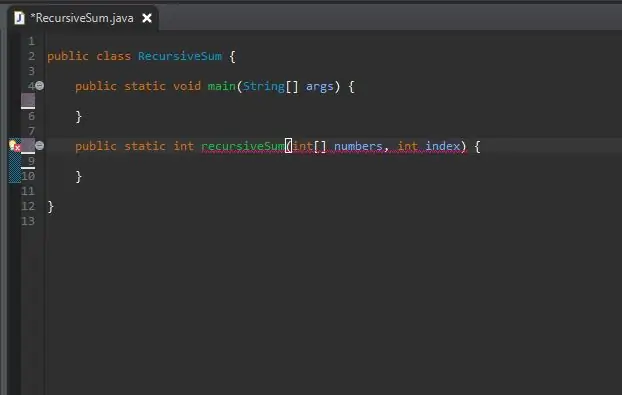
Ārpus galvenās metodes izveidojiet rekursīvās metodes metodes galveni.

Metode ir statiska, jo tai nav nepieciešams izmantot objektu.

Atgriešanās veids ir int, jo mūsu izmantotais masīvs būs pilns ar veseliem skaitļiem. Tomēr to var mainīt uz jebkura veida masīvu.

Esmu nosaucis savu metodi recursiveSum, kurai būs divi parametri; veselu skaitļu masīvs un indekss, ko mēs summai pievienosim. Es šos parametrus nosaucu attiecīgi par skaitļiem un indeksu.

Jūs tūlīt redzēsit kļūdas, un tas ir labi. Tie tiks laboti vēlāk.

3. darbība. Izveidojiet savu Kicker/pamata lietu

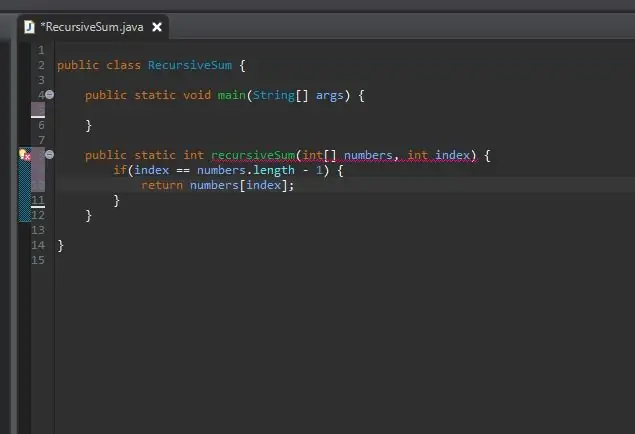
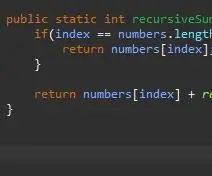
Rekursīvai metodei ir nepieciešams kicker/bāzes gadījums. Tas ir nosacījums, kas neļaus jūsu metodei bezgalīgi saukties. Šo pamata lietu var uzskatīt par vienkāršāko gadījumu, ar kuru mēs saskarsimies. Šajā gadījumā pamata gadījums būs tad, kad būsim mūsu masīva beigās. Ja pašreizējais indekss ir vienāds ar masīva garumu (mīnus 1, jo masīvi sāk skaitīt no 0 nevis 1), mēs esam beigās un mēs vienkārši atgriežam šo elementu šajā indeksā.

4. solis: rekursīvais solis

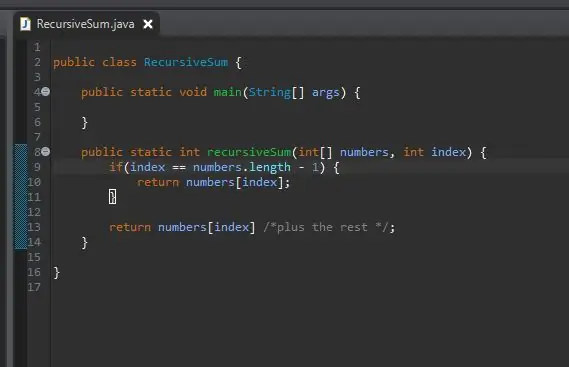
Kad mums ir pamatlietas, nākamais solis ir mūsu rekursīvais solis. Šeit notiek maģija. Mēs esam apstrādājuši gadījumu, kad mūsu indekss ir vienāds ar mūsu masīva pēdējo elementu. Ko darīt, ja mēs neesam pēdējā masīva elementā? Ko darīt, ja mēs varētu vienkārši pateikt, lai pievienotu mūsu pašreizējo elementu un nākamo? Galu galā mēs sasniegsim mūsu masīva beigas, un mūsu pamata gadījums ietekmēs.

Lai to paveiktu, mēs vienkārši atgriežam pašreizējo indeksu un “pievienojam pārējo” masīvam.

5. solis: saīsiniet problēmu

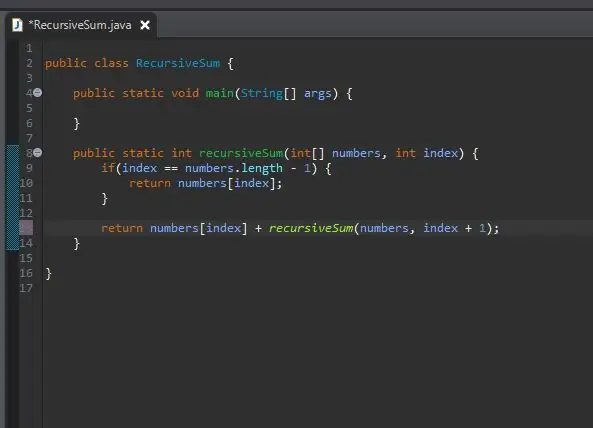
Kā mēs vienkārši "pievienojam pārējo"? Mums jau ir metode, kas pievienos noteiktu elementu; mūsu recursiveSum () metode! Mēs to varam saukt vēlreiz, bet mainām, kuru indeksu apkopojam.

Mēs nododam tajā pašā masīvā, kuru mēs apstrādājam, bet mēs ievadām nākamo indeksu no mūsu pašreizējā indeksa. Mēs to darām, vienkārši pievienojot vienu mūsu pašreizējam indeksam, kā parādīts attēlā.

6. darbība: izveidojiet veselu skaitļu masīvu

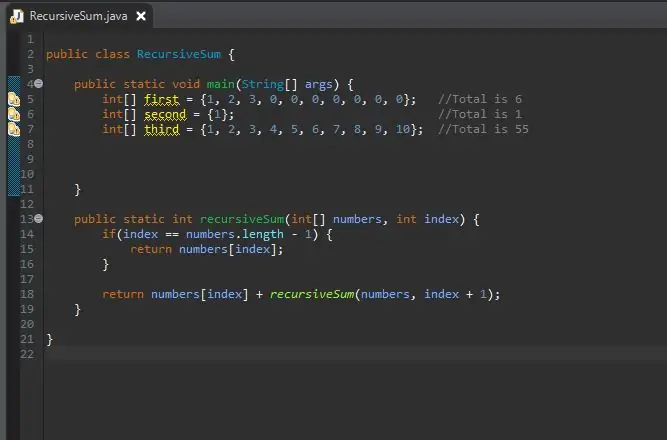
Tagad, kad mūsu rekursīvās summēšanas metode ir pabeigta, mēs varam izveidot savu masīvu, ko mēs apstrādāsim. Šis masīvs būs mūsu galvenajā metožu blokā.

Jūs varat izveidot masīva izmēru tik ilgi, cik vēlaties. Esmu izveidojis dažus dažādus masīvus ar dažādiem izmēriem un vērtībām, lai parādītu, ka tas darbojas ne tikai vienā izmērā.

7. solis: izsauciet metodi ar saviem masīviem

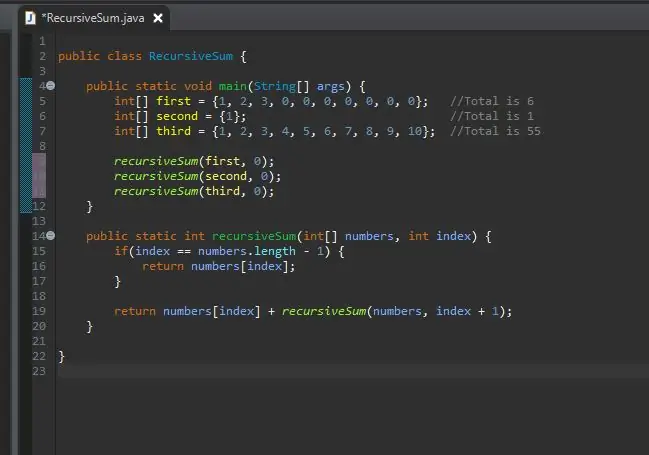
Tagad jūs varat izsaukt savu rekursīvo metodi un nodot tai šos masīvus. Tagad jūs varat palaist savu programmu.

8. darbība: izdrukājiet rezultātus

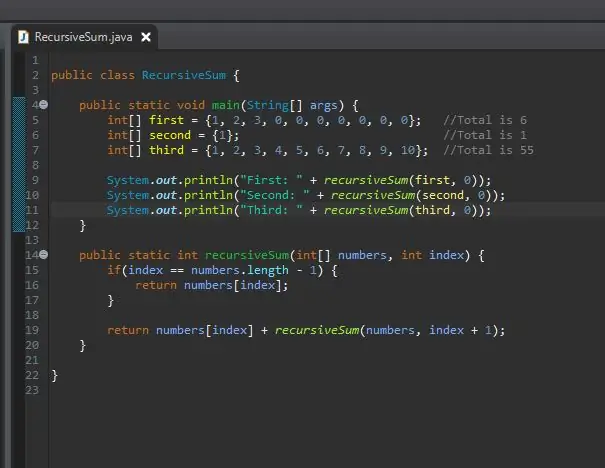
Nekas nav noticis. Kāpēc? Rekursīvā summa atgriež veselu skaitli, bet mēs neesam darījuši neko ar šo veselu skaitli. Tas darīja savu darbu, bet mēs nevaram redzēt rezultātu. Lai redzētu rezultātu, mēs to vienkārši izdrukājam. Pēc šī palaišanas jums vajadzētu redzēt katra jūsu masīva rezultātus.

9. solis: Apsveicam

Jūs esat pabeidzis rekursīvu funkciju. Jūtieties brīvi mainīt savu masīvu lielumu. Ja to pārbaudīsit, pamanīsit, ka tas avarē, ja jums ir tukšs masīvs. Mēs to neesam uzskaitījuši, taču tas ir lielisks veids, kā uzlabot rekursīvo metodi.