Patiesības tabulu risināšana: 10 soļi

2024 Autors: John Day | [email protected]. Pēdējoreiz modificēts: 2024-01-30 10:52

Patiesības tabula ir veids, kā vizualizēt visus problēmas rezultātus. Šis instrukciju komplekts ir paredzēts cilvēkiem, kuri sāk apgūt diskrēto matemātiku. Mēs šodien praktizēsim ar problēmu piemēru, kas raksturīgs šīm instrukcijām. Lai vizualizētu galdu, jums būs nepieciešams papīrs un zīmulis. Šīs problēmas risināšanai vajadzētu ilgt aptuveni 5 minūtes cilvēkiem ar priekšzināšanām par šo tēmu un aptuveni 10 minūtēm iesācējiem.

Šajā instrukciju komplektā mēs koncentrēsimies uz problēmu ~ p Λ q. Mēs to izmantojam, lai ieviestu dažus simbolus, kas nepieciešami patiesības tabulu interpretēšanai.

1. darbība. Izprotiet patiesības tabulas

Patiesības tabula ir veids, kā vizualizēt visas problēmas iespējas. Patiesības tabulu apzināšana ir diskrētas matemātikas pamatvajadzība. Šeit mēs atradīsim visus vienkāršā ~ p Λ q vienādojuma rezultātus.

2. solis: Zinot simbolus

Pirmais solis uz patiesības tabulu ir zīmju izpratne. “~” Šajā konkrētajā problēmā nozīmē noliegšanu. Gan “p”, gan “q” ir mainīgie. “Λ” ir līdzvērtīgs “un”. Šis vienādojums tiek lasīts kā “nevis p un q”, kas nozīmē, ka vienādojums ir patiess, ja p nav patiess un q ir patiess.

3. darbība: tabulas formatēšana

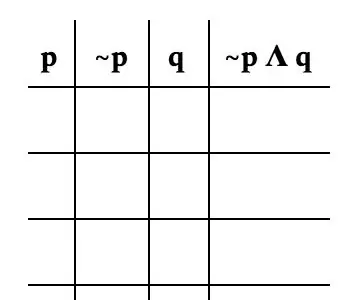
Tagad, lai izveidotu faktisko tabulu. Ir svarīgi sadalīt problēmu pēc katra mainīgā. Lai atrisinātu šo problēmu, mēs to sadalīsim šādi: p, ~ p, q un ~ p Λ q. Attēls ir labs piemērs tam, kā jāizskatās jūsu galdam.

4. solis: piešķiriet patiesu un nepatiesu

Tā kā ir tikai divi mainīgie, katram mainīgajam būs tikai četras iespējas. Attiecībā uz p mēs to sadalām ar pusi atstarpēm, ko aizņem T (patiesai), bet otru pusi - F (nepatiesai).

5. solis: noliegums

Attiecībā uz ~ p jūs rakstāt pretēju zīmi, kāda p ir, jo ~ p ir pretstats p.

6. darbība: mainīgais “q”

Attiecībā uz q jūs maināt T un F, lai iegūtu katru iespējamo kombināciju. Tā kā vienādojums koncentrējas tikai uz ~ p, mēs varam ignorēt kolonnu p, nosakot vienādojuma patiesumu. Simbols “Λ” nozīmē, ka vienībai ~ p un q ir jābūt patiesai, lai vienādojums būtu patiess.

7. darbība. Nepareiza risināšana pēdējā slejā

Pirmajā rindā, tā kā ~ p ir F un q ir T, ~ p Λ q ir F scenārijā, kad ~ p ir F un q ir T. Vienīgais scenārijs, kur vienādojums ir T, kur ~ p ir T un q ir T.

8. darbība. Patiesības atrašana pēdējā slejā

Tas nozīmē, ka vienīgā T rinda ir trešā.

9. solis: Galda apdare

Vēlreiz pārbaudiet, vai jūsu tabula ir pareiza. Jūs to darāt, pārbaudot, vai jūsu zīmes ir pareizas, un pārliecinoties, ka pēdējā sleja ir izdarīta pareizi. Pēdējā kolonna ir visu iespējamo mainīgo izmaiņu rezultāts.

10. darbība. Gatavs

Tagad, kad jūs zināt, kā sastādīt pamata patiesības tabulu, turpiniet praktizēt! Jo vairāk jūs praktizēsit, jo labāk jūs tos izpildīsit.