3D rekonstrukcija no viena fotoattēla: 8 soļi

2024 Autors: John Day | [email protected]. Pēdējoreiz modificēts: 2024-01-30 10:51

3D rekonstrukcijas uzdevums parasti ir saistīts ar binokulāro redzi. Alternatīvi, jūs varat pārvietot vienu kameru ap objektu. Tikmēr, ja objekta forma ir zināma, uzdevumu var atrisināt no vienas fotogrāfijas. Tas nozīmē, ka jums ir tikai viena kamera, un tā nekustās. Apskatīsim, kā to izdarīt soli pa solim. Mēs izmantosim Rubika kubu, jo tas ir labi standartizēts un tam ir bagātīgs funkciju kopums. To var uzskatīt par ļoti vienkāršu objektu un vienlaikus sarežģītu konstrukciju. Tātad mašīnas redzei ir jāpārvar būtiski šķēršļi, lai veiktu uzdevumu.

1. darbība: novērtējiet uzdevuma sarežģītību

No pirmā acu uzmetiena uzdevums ir vienkāršs. Atrodiet centrālo mezglu, kurā sakrīt 3 kuba malas, un uzzīmējiet šīs malas. Pēc to koordinātām ir iespējams aprēķināt attālumu no kameras un rotācijas leņķus. Problēma ir tāda, ka šīs līnijas nepastāv. No kreisā attēla redzat, ka katru malu attēlo 2 paralēlas līnijas. Turklāt augšējā labajā attēlā redzams, ka katrs no tiem ir sadalīts 3 segmentos. Turklāt, ja mēs izmantojam populārās Hough transformācijas variantu, kas var noteikt līniju segmentus, tas veic uzdevumu ar dažām kļūdām, kas padara centrālā mezgla noteikšanu neiespējamu. Ja gali nesasniedz viens otru, nav viena punkta. Ja noteikšana pārspēj galu, tas izskatīsies kā mezgls malas vidū, kā redzat 2 atlikušajos attēlos.

2. darbība: atrodiet pareizo pieeju

Ja pārāk daudz detaļu padara deterministiskus algoritmus neiespējamus, ir pienācis laiks apsvērt varbūtības pieeju. Ja mēs aprēķinām attēla vidējos parametrus, to kļūdas tiks ievērojami samazinātas, un paradoksāli šī metode izrādīsies ticamāka. Standarta Hough transformācija neizvada līniju segmentus. Tikai tā slīpums teta un attālums rho no koordinātu sākuma. Tie veido Hough kosmosa daļu, kuras daļa ir parādīta iepriekš. Šeit teta atbilst horizontālajai asij. Spilgti plankumi iezīmē iespējamās līnijas attēlā. Ņemiet vērā, ka vairākas šādas vietas atrodas viena virs otras. Nav brīnums, ka mūsu attēlā ir daudz paralēlu līniju. Viņiem ir viena un tā pati teta un dažādi rho.

3. solis: aprēķiniet teta histogrammu

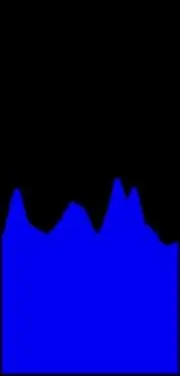
Atklāsim šādas kopas. Šim nolūkam mēs apkoposim visu Hough telpas punktu rādījumus ar vienu un to pašu teta. Attēlā redzama atbilstošā histogramma. Dažas piezīmes par mērījumiem. Strādājot ar attēliem pikseļu koordinātās, X ass iet kā parasti, bet Y norāda uz leju, tāpēc koordinātu izcelsme ir augšējais kreisais stūris, un teta jāmēra no X ass pulksteņrādītāja virzienā. Paturot prātā, ka viss attēla teta slīpums ir 180 grādi, varat aptuveni pārbaudīt, vai trīs galvenās virsotnes attēlo trīs attēla galvenās nogāzes.

4. solis: aprēķiniet Rho histogrammu

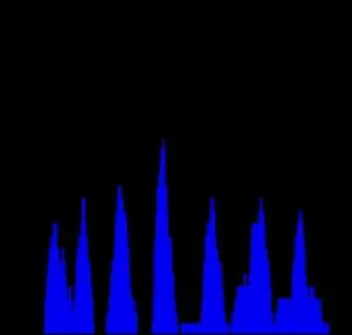
Tagad, kad mēs zinām trīs galvenās paralēlu līniju kopas, atdalīsim līnijas katrā no tām. Mēs varam atkārtot to pašu pieeju. Paņemsim kolonnu no Hough telpas, kas atbilst vienai teta histogrammas virsotnei. Tālāk mēs aprēķināsim citu histogrammu, kur X ass apzīmē rho vērtību un Y - apkopotos rādījumus šim rho. Acīmredzot summa būs mazāka, tāpēc šī diagramma nav tik gluda. Tomēr virsotnes ir skaidri redzamas, un to skaits (7) precīzi atbilst avota attēla paralēlo līniju skaitam. Diemžēl ne visas diagrammas ir tik perfektas, taču princips ir skaidrs.

5. darbība: atrodiet centrālo mezglu

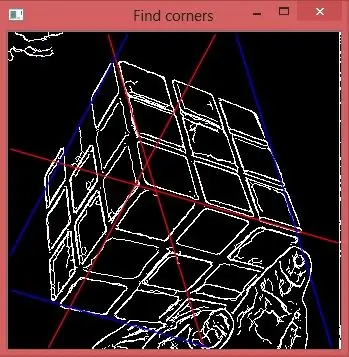
Ja katrai tetai ņemsim rho histogrammas centrālo maksimumu, mēs iegūsim 3 līnijas, kas attēlā ir sarkanas. To krustojums iezīmē nepieciešamo punktu.

6. darbība: izvēlieties no 2 alternatīvām

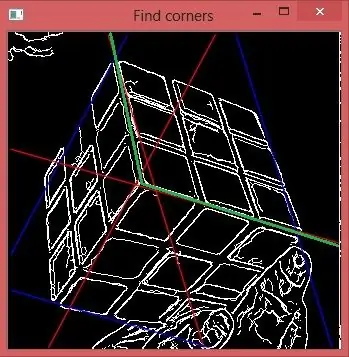
Jūs redzat, ka katra līnija iet no centrālā punkta abos virzienos. Kā noteikt pareizo pusi? Ņemsim teta3. Pieņemsim, ka mēs ņemam šīs līnijas apakšējo daļu. Aprēķināsim vēl vienu Hough vietu tikai attēla daļai no 2 zaļām līnijām līdz attēla augšējam labajam stūrim. Pēc tam izveidojiet tai teta histogrammu. Jūs redzat, ka trešā virsotne pilnībā pazuda, tāpēc esam izdarījuši pareizo izvēli.

7. solis: nosakiet ārējos stūrus

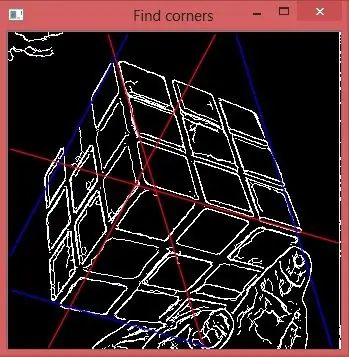
Tagad mēs varam izmantot pirmo un pēdējo pīķi rho histogrammās, lai uzzīmētu zilas līnijas, kas nogriež sarkanās malas un iezīmē pārējos stūrus. Uzdevums ir atrisināts.

8. solis: izmēģiniet to praksē

Šīs instrukcijas ilustrācijas tika izveidotas, izmantojot Perception 1.0. Šī ir bezmaksas programmatūra, kas izmanto OpenCV - jaudīgu bibliotēku datora redzei. Tas var būt saistīts arī ar WinNB, kas tika izmantots manā citā Instructable, tādējādi nodrošinot redzes iespējas robotikai. Abas programmas varat lejupielādēt no vietnes nbsite. Instalēšanai vienkārši palaidiet lejupielādēto exe failu. Vēlāk to var noņemt, izmantojot Windows standarta rīku. Vietnē ir arī resursi par datoru redzi un saistītām tēmām. Uztverē jūs atradīsit aprakstīto 3D rekonstrukcijas metodi, kā arī daudzas citas. Šīs programmas priekšrocība ir tā, ka tā izvada gala rezultātu kopā ar starpposma datiem. Jūs varat izpētīt, kā darbojas datora redze, nebūdams programmētājs. Attiecībā uz ievadi katrā metodē ir īpaši atlasīti tipiski paraugi. Protams, jūs varat izmantot arī savu. Ir iespējams ievadīt attēlus no faila vai no datora kameras. Jūtieties brīvi sazināties ar mani, ja jums ir kādi jautājumi vai ieteikumi.