Acu ābola recepte: BME60B projekts: 9 soļi

2024 Autors: John Day | [email protected]. Pēdējoreiz modificēts: 2024-01-30 10:51

Autori: Hanna Silos, Sang Hee Kim, Thomas Vazquez, Patrick Viste

Palielinājums ir viena no galvenajām lasīšanas brilles iezīmēm, kuras klasificē pēc dioptriju izrakstīšanas. Saskaņā ar Mičiganas Tehnoloģiju universitāti, dioptrija ir objektīva fokusa attālums, ko parasti mēra mm, metru vienībā (Mičiganas Tehnoloģiju universitāte). Tā kā lasīšanas brillēm ir izliektas lēcas, fokusa attālums būtu pozitīvs, kā rezultātā arī dioptrijas būtu pozitīvas (HyperPhysics). Fokusa attālums palielinās, attālumam starp objektu attālinoties no faktiskā objektīva, un tas noved pie dioptriju samazināšanās, jo tās ir apgriezti proporcionālas. Tāpēc lasīšanas brilles ar papildu dioptrijām palīdzētu objektīvam tuvināt skatu tā, lai varētu šķist, ka fokusa attālums ir mazāks, palielinot dioptriju vērtību.

Uzrādītais kods tiks izmantots, lai prognozētu lēcas dioptriju ar nezināmu recepti. Lai aprēķinātu recepti, tiek izmantotas divas ievades: kontrolēta fona fotogrāfija, neizmantojot objektīvus, un cita tā paša fona fotogrāfija, bet caur izvēlēto objektīvu. Programma mērīs izkropļojumus starp šīm divām fotogrāfijām. No turienes mēs varēsim novērtēt objektīva dioptriju un radīt rezultātu, ko lietotājs var apskatīt.

Lai iegūtu šo pamācību, jums būs nepieciešams:

• Melnbalts šaha galdiņa raksts, kas iespiests uz papīra lapas 11x8,5
• Kamera ar iespēju fiksēt fokusu
• Statīvs vai kaut kas līdzīgs kameras nostiprināšanai
• Dažādas lasīšanas brilles receptes
• MATLAB

1. darbība: uzņemiet fotoattēlus

Lai aprēķinātu objektīva palielinājumu, jums jāspēj to salīdzināt ar faktisko objekta izmēru. Šim projektam mēs salīdzināsim palielinātu attēlu ar kontroles attēlu.

Tādējādi pirmais solis ir uzņemt divus viena un tā paša attēla fotoattēlus - pirmo tikai caur kameru, bet otro - caur lasāmo brilles objektīvu, kuru vēlaties pārbaudīt.

Jūs fotografēsit 8,5x11 collu melnbalto šaha galdu ar 1 collu režģi. Iestatiet kameru 11 collu attālumā no šaha dēļa. Pirms fotoattēlu uzņemšanas fiksējiet šaha tabulu.

Nofotografējiet šaha galdu bez lasīšanas brillēm. Pēc tam, neko nekustinot, novietojiet lasīšanas brilles kameras priekšā un uzņemiet otro fotoattēlu.

Pārliecinieties, ka kameras pozīcija nepārvietojas starp kadriem. Vienīgais, kam vajadzētu mainīties starp abām fotogrāfijām, ir brilles objektīva klātbūtne kameras priekšā.

Kad esat pabeidzis ar fotoattēliem, augšupielādējiet tos savā datorā.

2. darbība. Ielādējiet attēlus MATLAB

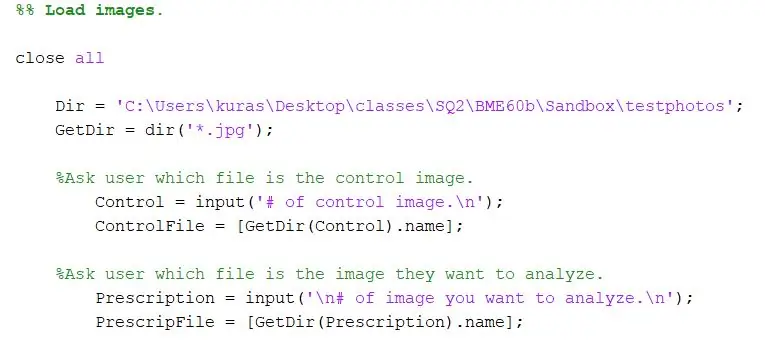
Atveriet jaunu skriptu.

Vispirms norādiet direktoriju, kurā tiek glabāti fotoattēli. Pēc tam izmantojiet funkciju dir, lai izvilktu-j.webp

Dir = 'C: / Users / kuras / Desktop / class / SQ2 / BME60b / Sandbox / testphotos'; GetDir = dir ('*. Jpg');

Mūsu projektam mēs vēlējāmies norādīt programmas lietotājam, kurus failus viņi vēlas salīdzināt. Pirmajā sadaļā lietotājam tiek lūgts norādīt kontroles attēlu, bet otrajā - lietotājam jānorāda testa attēls.

• %Jautājiet lietotājam, kurš fails ir kontroles attēls.
• Kontrole = ievade ('kontroles attēla#. / N');
• ControlFile = [GetDir (Control).name]
• %Jautājiet lietotājam, kurš fails ir attēls, kuru viņi vēlas analizēt.
• SelectFile = input ('\ n# no attēla, kuru vēlaties analizēt. / N');
• PrescripFile = [GetDir (Izvēlēties failu). Nosaukums];

3. darbība: attēlu analīze

Krāsains attēls MATLAB ir MxNx3, bet pelēktoņu attēls ir MxN. Tas nozīmē, ka ir ātrāk uzlabot/rediģēt pelēktoņu attēlu, jo ir mazāk datu, ko izsekot. Izmantojiet rgb2gray, lai attēlu pārvērstu pelēktoņos. (Funkcija imrotate tika izmantota, jo mūsu fotoattēli bija horizontāli - šī koda rindiņa var būt vai nebūt nepieciešama jūsu versijā.)

• %pārvēršas pelēktoņos un pagriež
• I = imread (ControlFile);
• I = rgb2pelēks (I);
• I = imrotēt (I, 90);

Pēc tam parādiet attēlu. Apakšplāna funkcija tiek izmantota, lai testa attēls turpmākajās darbībās varētu atrasties blakus vadīklai.

• %displejs
• attēls (1);
• apakšplāksne (1, 2, 1)
• imshow (I);
• nosaukums (ControlFile);

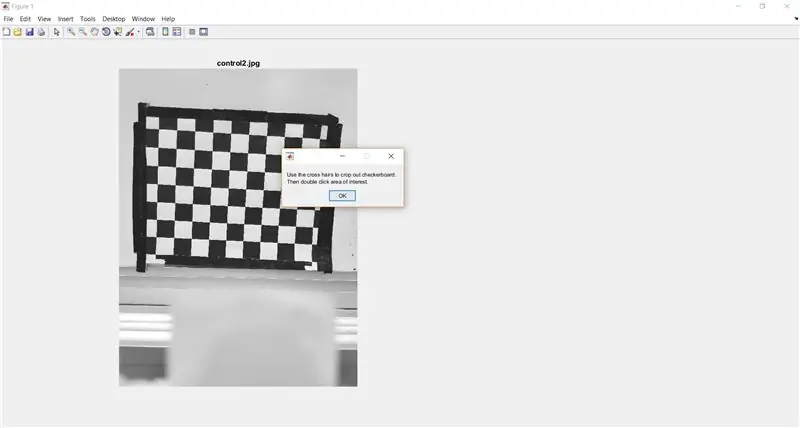
Izmantojiet imcrop, lai pamudinātu lietotāju apgriezt rūtiņu no visa attēla. Tālāk norādītajā kodā tiek parādīts arī ziņojumu lodziņš, lai sniegtu norādījumus lietotājam.

• %apgriezt pārbaudītāju tabulu analīzei
• waitfor (msgbox ({'Izmantojiet krustu, lai izgrieztu rūtiņu.', 'Pēc tam veiciet dubultklikšķi uz interesējošā apgabala.'});
• I_crop = imcrop (I);

Izmantojiet imbinarize, lai binarizētu attēlu.

I_binary = imbinarize (I_crop);

4. solis: aprēķiniet šaha laukuma balto kvadrātu platumu

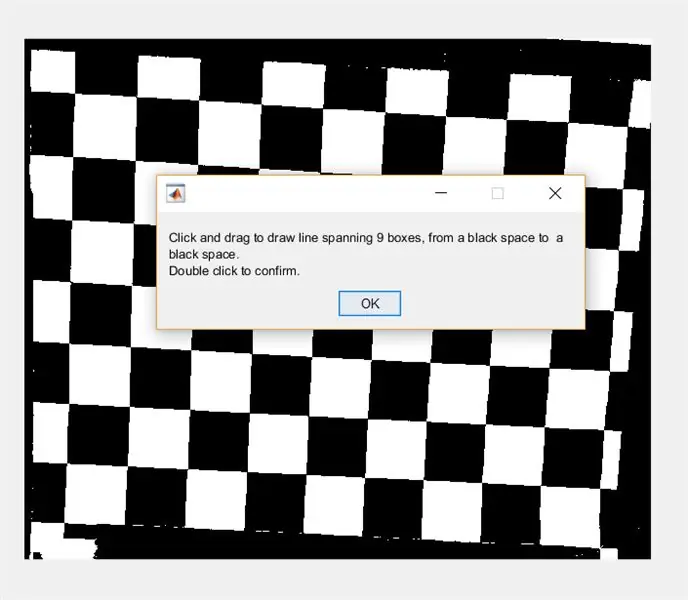
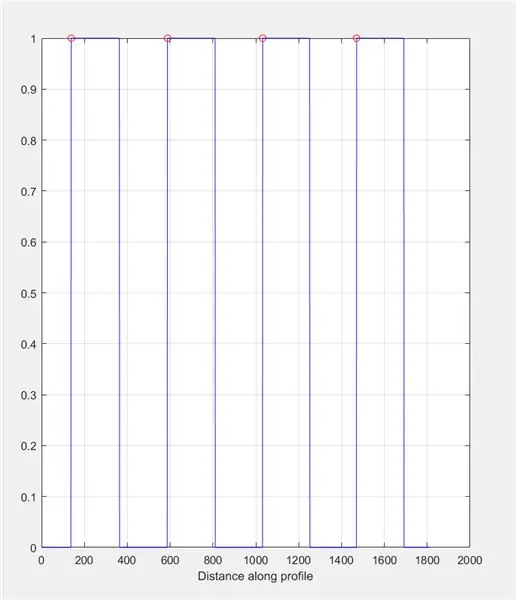
Pēc tam pamudiniet lietotāju uzzīmēt līniju pāri attēlam, izmantojot imline. Šai līnijai jāiet horizontāli pāri šaha galdiņam. Tam vajadzētu sākties un beigties uz melna kvadrāta (nav svarīgi, kur)- tas ir tāpēc, ka mēs mērīsim balto, nevis melno kvadrātu platumu.

• %novilkt līniju
• attēls (1)
• apakšplāksne (1, 2, 1)
• imshow (I_binary);
• waitfor (msgbox ({'Noklikšķiniet un velciet, lai novilktu līniju, kas aptver 9 kastes, no melnas vietas uz melnu atstarpi.', 'Veiciet dubultklikšķi, lai apstiprinātu.'});
• līnija = imline;
• pozīcija = gaidīt (rinda);
• galapunkti = line.getPosition;

Izvelciet X un Y kodinātus novilktās līnijas galapunktiem.

• X = galapunkti (:, 1)
• Y = galapunkti (:, 2);

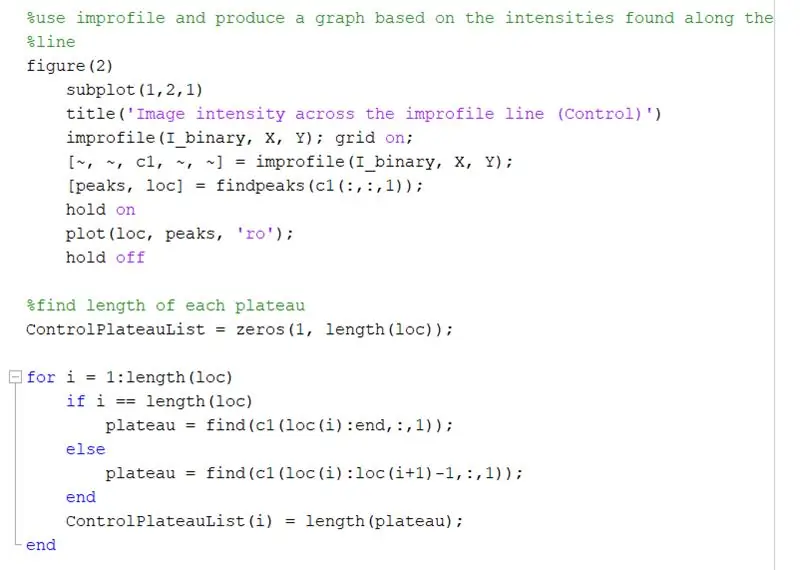
Izmantojiet improfile, lai izveidotu grafiku, pamatojoties uz intensitāti, kas konstatēta gar novilkto līniju. Tam vajadzētu atgādināt kvadrātveida vilni no 0 (melns) līdz 1 (balts). Aprēķiniet arī virsotnes un to atrašanās vietas.

• attēls (2)
• apakšplāksne (1, 2, 1)
• virsraksts ('Attēla intensitāte visā improfile līnijā (Control)')
• improfile (I_binary, X, Y); režģis ieslēgts;
• [~, ~, c1, ~, ~] = improfile (I_binary, X, Y);
• [virsotnes, loc] = atradumi (c1 (:,:, 1));
• uzgaidi
• gabals (loc, virsotnes, 'ro');
• turies

Atrodiet katra plato garumu improfile grafikā, izmantojot for cilpu. Palaidiet for ciklu tādam pašam maksimumu skaitam, kāds ir improfile diagrammā. Lai aprēķinātu katra plato garumu, izmantojiet funkciju “atrast”, lai atrastu visas vietas, kur ir “1”, nevis “0” intensitātes vērtība. Pēc tam aprēķiniet šī masīva garumu, lai iegūtu plato kopējo garumu, kam vajadzētu būt vienādam ar balta kvadrāta platumu pikseļos. ControlPlateauList = nulles (1, garums (loc));

i = 1: garums (loc)

ja i == garums (loc)

plato = atrast (c1 (loc (i): beigas,:, 1));

citādi

plato = atrast (c1 (loc (i): loc (i+1) -1,:, 1));

beigas

ControlPlateauList (i) = garums (plato);

beigas

5. darbība: atkārtojiet 3. un 4. darbību testa attēlam

*Piezīme: uzzīmējot improfile līniju uz testa attēla, noteikti zīmējiet to pāri kvadrātiem, kas atbilst līnijai, kuru uzzīmējāt uz kontroles attēla.

6. darbība: aprēķiniet objektīva palielinājumu

Palielinātos mērījumus aprēķina, dalot plato garuma vidējo lielumu, kas tika aprēķināts 5. solī, ar kontroles plato garuma vidējo lielumu, kas tika aprēķināts 4. solī. Tiek aprēķināts, ka tas ir 1,0884.

palielinājums = vidējais (plato saraksts)/vidējais (kontroles plato saraksts);

7. solis: atrodiet R kvadrātu un lietotāja recepti, izmantojot interpolāciju

Izmantojot kodu:

• md1 = fitlm (GivenPrescription, MagArray);
• Rsquared = md1. Rsquared. Ordinary;

Mēs varam atrast grafika R kvadrātā vērtību GivenPresciption (mūsu objektīviem dotās vērtības) pret MagArray (palielinājumu mērījumu attiecību masīvs, ko mēs aprēķinājām iepriekš). Ja R kvadrāta vērtība ir pietiekami augsta, var secināt, ka pastāv pietiekami spēcīga korelācija, lai pamatotu šīs metodes izmantošanu. Šajā konkrētajā gadījumā R kvadrāta vērtība bija 0, 9912, kas liecina par spēcīgu korelāciju, un tāpēc ir pamatoti izmantot šo metodi analīzē.

Izmantojot funkciju:

Recepte = interp1 (MagArray, GivenPrescription, palielinājums, 'lineārs');

Mēs varam interpolēt palielinājuma koeficienta atbilstošo recepšu vērtību (uz x ass) (vērtība uz y ass) un noskaidrot, kāda ir lietotāja recepte.

Datu interpolācija ir svarīga, lai šī metode darbotos, jo tā ļauj mums izdarīt pieņēmumus par informāciju, kuras mums nav, pamatojoties uz mūsu rīcībā esošo informāciju. Lai gan vispiemērotākā līnija tehniski būtu spēcīgāks kandidāts šim pieņēmumam, robežu izveidošana, lai samazinātu izvades gadījumu skaitu, kalpo tam pašam efektam, jo recepšu brillēm jebkurā gadījumā ir pakāpeniski vienādas vērtības. Tas ir izskaidrots turpmākajos soļos.

8. darbība. Lietotāja receptes parādīšana grafikā

Izmantojot šādu kodu:

• figūra;
• gabals (GivenPrescription, MagArray, '-g')
• uzgaidi
• gabals (recepte, palielinājums, “bp”)
• turies
• režģis
• leģenda ('Dati', 'Interpolētie punkti', 'Atrašanās vieta', 'ZR')

Mēs varam uzzīmēt diagrammu, kurā parādīta palielinājuma pakāpe pret noteikto recepti ar zaļu līniju un atrastie dati par mūsu aprēķināto palielinājumu, salīdzinot ar mūsu interpolēto recepti ar zilu zvaigzni. Pēc tam leģenda apzīmē nosaukumu, x asi un y asi un novieto leģendu augšējā kreisajā stūrī.

9. solis: sašauriniet recepti

Lai noapaļotu recepti, tiek izmantots šāds kods:

• ja recepte <= 1,125

  CalculatedPrescription = '1.0';

• elseif Recepte <= 1,375

  CalculatedPrescription = '1,25';

• elseif Recepte <= 1.625

  CalculatedPrescription = '1.5';

• elseif Recepte <= 1.875

  CalculatedPrescription = '1,75';

• elseif Recepte <= 2,25

  CalculatedPrescription = '2.0';

• elseif Recepte <= 2,625

  CalculatedPrescription = '2.5';

• elseif Recepte <= 3

  CalculatedPrescription = '2.75';

• elseif Recepte <= 3.375

  CalculatedPrescription = '3.25';

• citādi

  CalculatedPrescription = 'nezināms';

• beigas

Recepte, kas atrasta, izmantojot interpolāciju, ne vienmēr atspoguļo faktisko recepti - tas ir tāpēc, ka cilvēka kļūdas dēļ fotoattēla analīzē vienmēr būs nelielas atšķirības. Tādējādi mums ir nepieciešams šis solis, lai klasificētu faktisko recepti.

Izrakstītās receptes parasti sākas ar 1,0 dioptriju un to receptēs palielinās par 0,25, tāpēc pēc receptes aprēķināšanas mēs vēlamies noteikt recepti, kas vislabāk atbilst lietotājam. Pēc receptes aprēķināšanas mēs to pārbaudām dotajos If paziņojumos, lai pārbaudītu tās vērtību un noteiktu, kura recepte ir nepieciešama. Viss, kas ir mazāks vai vienāds ar 1,125, tad recepte ir 1,0. Viss, kas ir mazāks vai vienāds ar 1,375, recepte ir 1,25. Viss, kas ir mazāks vai vienāds ar 1,625, recepte ir 1,5. Viss, kas ir mazāks vai vienāds ar 1,845, recepte ir 1,75. Un tā tālāk.

Mums palielinās vērtības, jo mēs pārbaudām, vai vērtības ir mazākas par. Ja mēs vērtības samazinātu, tad pirmais, ja paziņojums visu laiku lasītu pirmo ja. Ja recepte ir mazākā, mēs vēlamies, lai tā uzreiz to atzītu par mazāko, tāpēc mēs sākām ar mazāko vērtību. Viss, kas pārsniedz augstāko vērtību, nozīmē, ka recepte nav mūsu datu diapazonā, tāpēc virkne “Nezināms” tiks nolasīta.