Kā izveidot Temcor stila ģeodēzisko kupolu programmā Autodesk Inventor: 8 soļi

2024 Autors: John Day | [email protected]. Pēdējoreiz modificēts: 2024-01-30 10:57

Šī apmācība parādīs, kā izveidot Temcor stila kupolu, izmantojot tikai nedaudz matemātikas.

Lielākā daļa šīs pamācības informācijas tika iegūta no TaffGoch reversās inženierijas attiecībā uz vecās Amundsenas-Skotas Dienvidpola stacijas sadalīšanas metodi, tāpēc milzīgs paldies viņam!

Būtiska Temcor kupolu priekšrocība ir to zemais unikālais statņu skaits - tas aritmētiski palielinās ar frekvenci, neatšķirībā no Dankana Stjuarta parastā triakontaedriskā ģeodēziskā režģa (3. metode*), bet rezultāts izskatās daudz patīkamāks.

Vienkāršības labad mūsu izgatavotā kupola frekvence ir 14, tāpēc akordu faktorus var salīdzināt ar TaffGoch Temcor modeli.

Inventor 2016.ipt ir iekļauts apmācības beigās.

*ATJAUNINĀT*

Es aprakstīju 4. metodi kā Dankana Stjuarta parasto triakontaedrisko ģeodēzisko režģi, bet tā nav. Metodi patiesībā izgudroja Kristofers Kitriks, kurš savā 1985. gada darbā "Ģeodēziskie kupoli" aprakstīja tās uzbūvi. Turklāt 1990. gada rakstā "Vienota pieeja I, II un III klases ģeodēziskajiem kupoliem" viņš izklāsta vēl 8 metodes, no kurām viena ir Dankana Stjuarta 3. metode, otra - viņa 4. metode. pietiekami, metode, kas ir analoga Temcor metodei, ko viņš sauc par "aa metodi" (7. solis parāda, kā Temcor modificēja "metodi aa"). Turpmākā pamācībā es aprakstīšu pēdējā rakstā izklāstīto metožu uzbūvi.

1. darbība: lietotāja parametri

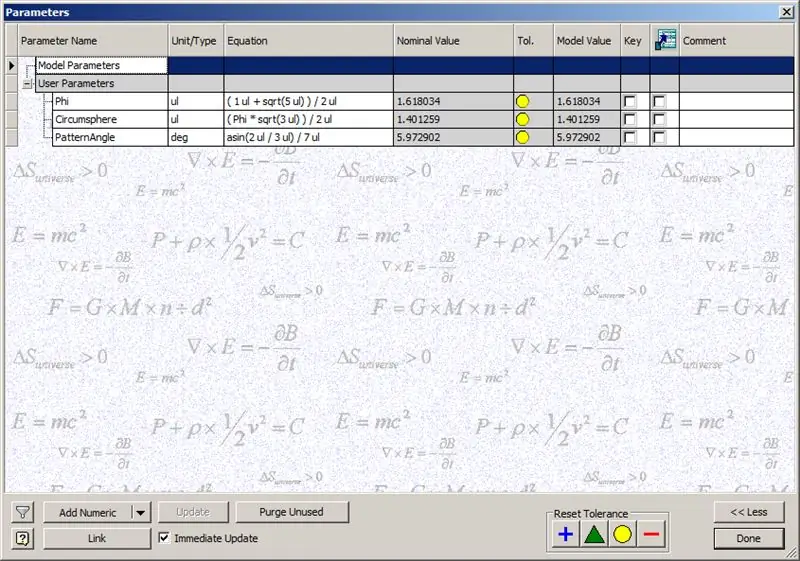
Pirms sākam būvēt kupolu, ievadiet parādītos parametrus:

Phi - zelta attiecība. Definēts kā ((1+√5/) 2

Apkārtmērs - šī ir dodekaedra aplis, kas definēts kā ((Phi*√3)/2)

PatternAngle - Šis ir dodekaedra centrālais leņķis. Tā kā mūsu kupola frekvence ir 14, mēs sadalām šo centrālo leņķi ar pusi frekvences, šajā gadījumā - 7.

2. darbība. Zelta taisnstūra ieskicēšana

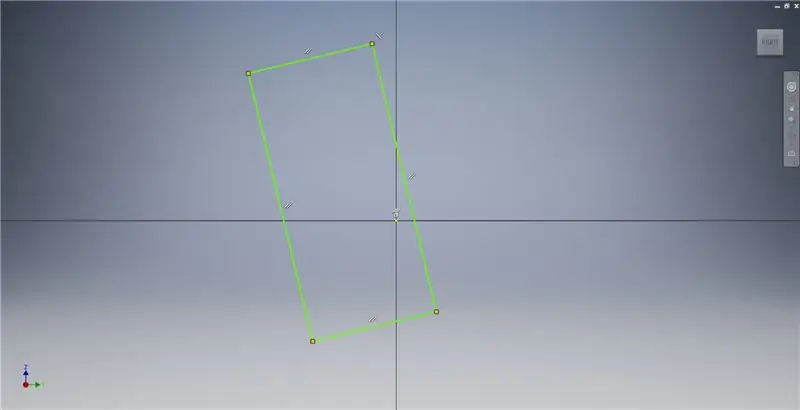
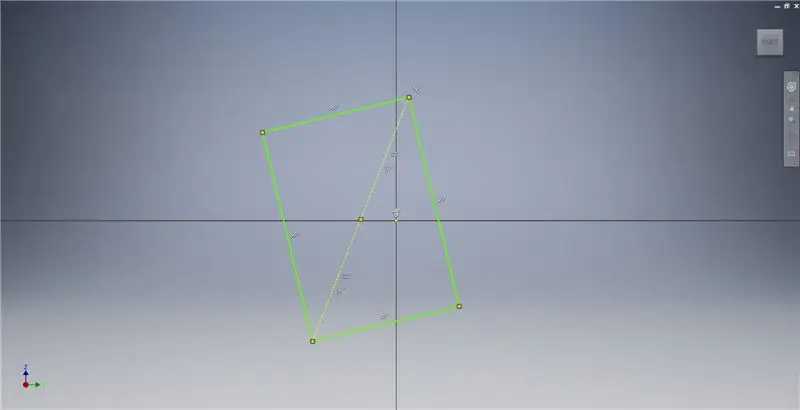
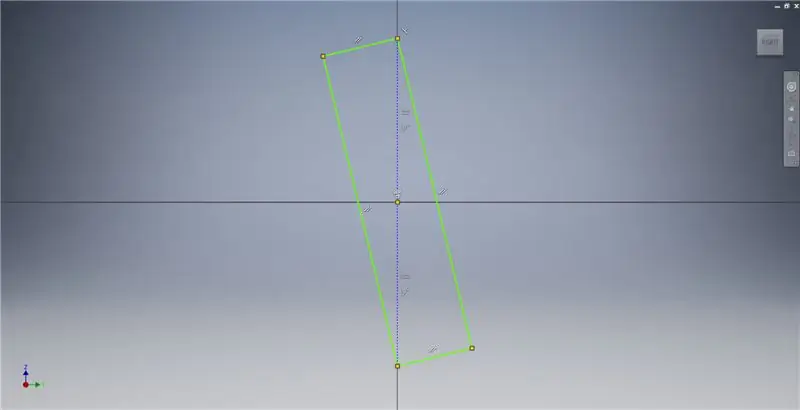
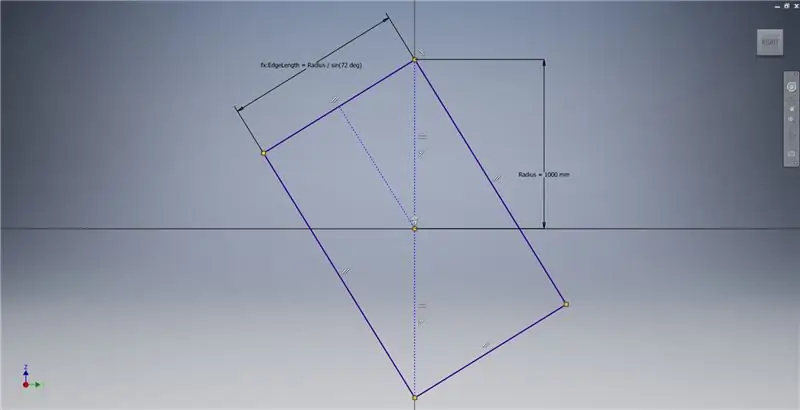
Sāciet skici YZ plaknē, pēc tam izveidojiet trīs punktu taisnstūri, kā parādīts attēlā, atsaucoties uz attēla piezīmēm, lai iegūtu papildinformāciju par zelta taisnstūra izveidi.

3. darbība. Zelta² taisnstūra izveide

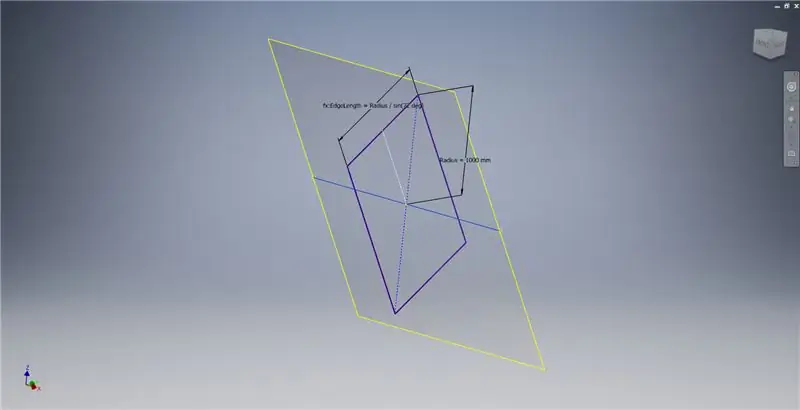
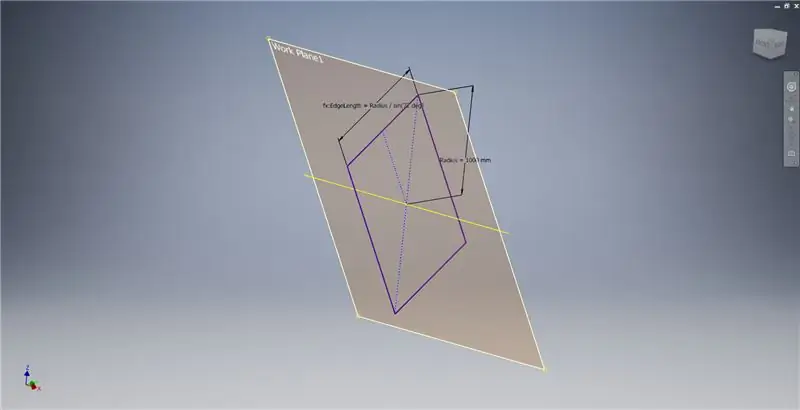
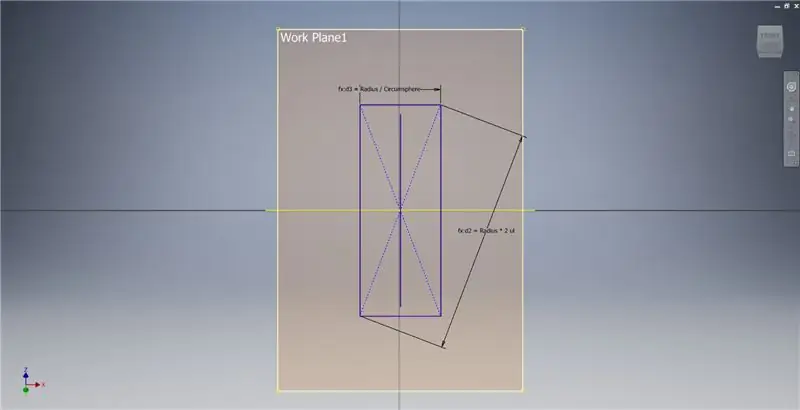
Izveidojiet apstrādes plakni, izmantojot X asi un pirmajā attēlā iezīmēto līniju, pēc tam sāciet citu skici šajā darba plaknē. Izveidojiet centra punkta taisnstūri, sākot ar sākumpunktu, un pēc tam izmēriet taisnstūri, kā parādīts trešajā attēlā.

4. solis: izveidojiet 2v Triacon trīsstūri

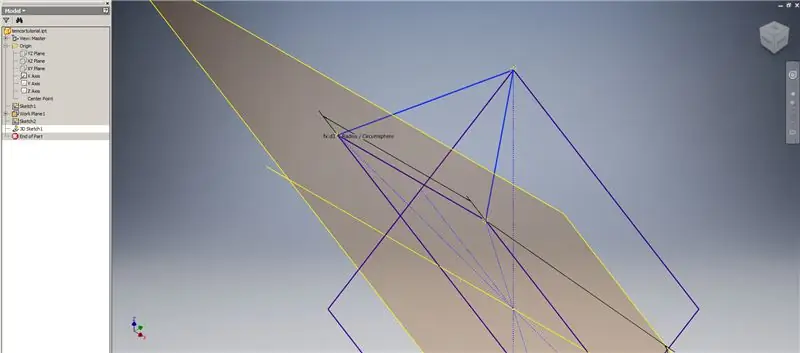
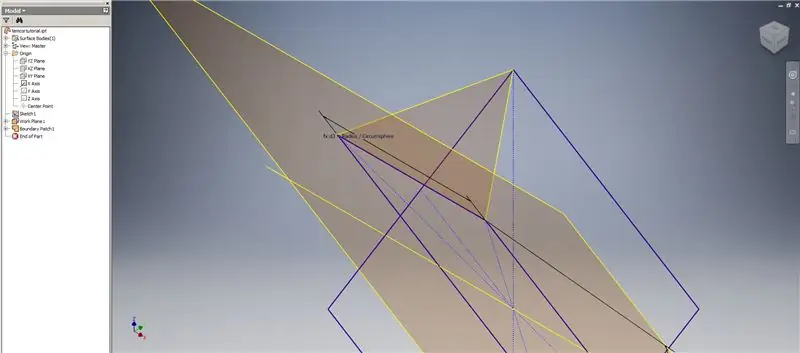
Tagad, kad mums ir visa nepieciešamā ģeometrija, otrajā attēlā izveidojiet robežas plāksteri, izmantojot jebkuru vēlamo metodi. Es izvēlējos izveidot 3D skici, bet skicēšana citā darba plaknē derētu tikpat labi.

5. solis: krustošanās plakņu izveide

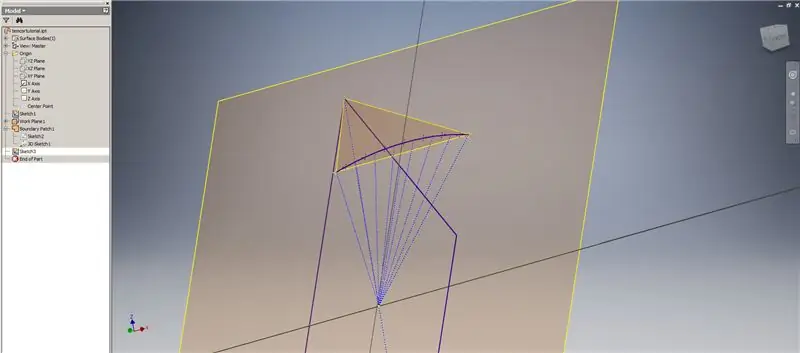
Sāciet citu skici pirmajā izveidotajā darba plaknē ("Darba plakne 1"), projicējiet Zelta² taisnstūra stūrus, pēc tam savienojiet šos punktus un sākumpunktu, lai izveidotu 2v triakontaedra centrālo leņķi. Sadaliet to uz pusi no kupola frekvences, it kā sāktu 2. metodes sadalījumu. Novietojiet punktus uz akordu viduspunktiem.

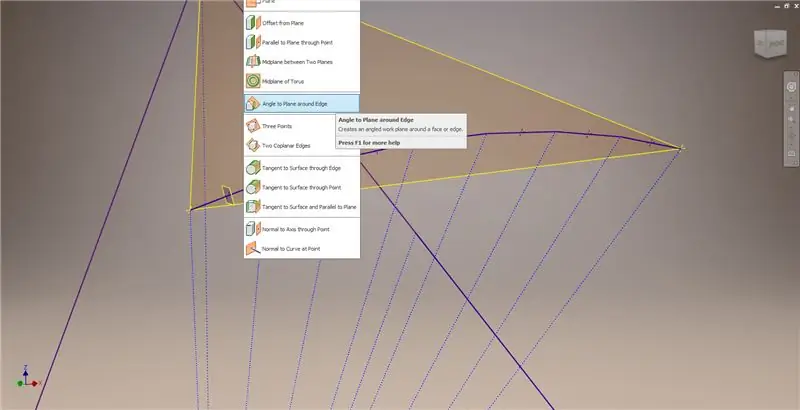
Izejiet no skices, pēc tam izveidojiet plakni, izmantojot vienu no akordiem un tā viduspunktu, kā parādīts otrajā attēlā. Pēc tam izveidojiet citu darba plakni, izmantojot leņķi pret plakni ap malu. Atlasiet 1. darba plakni un vienu no konstrukcijas līnijām, kas parādītas labajā vidū un apakšējā kreisajā attēlā. Pieņemiet noklusējuma leņķi 90 grādi, pretējā gadījumā pārējā apakšiedaļa neizskatītos pareizi. Atkārtojiet procesu, izmantojot pārējos akordus un konstrukcijas līnijas, lai iegūtu rezultātu labajā apakšējā attēlā.

6. darbība: krustošanās līkņu izveide un apakšnodaļas veidošana

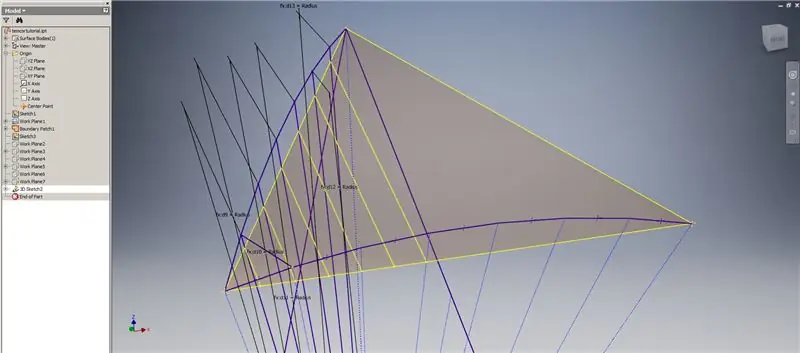
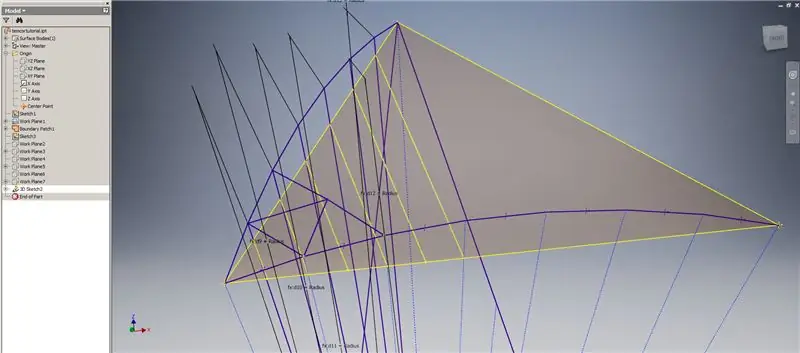
Sāciet 3D skici, pēc tam izveidojiet krustošanās līknes, izmantojot tikko izveidotās darba plaknes un robežu plāksteri, veidojot augšējā attēlā redzamās līnijas.

Zīmējiet līnijas, kas sakrīt ar krustošanās līkņu galapunktiem, kā parādīts 2. attēlā. Padariet tās visas vienādas ar kupola rādiusu. Uzzīmējiet akordus, kas savieno līnijas, kas atrodas uz krustošanās līknēm. Savienojiet jebkuru ģeometriju, kas izskatās pietiekami tuvu, lai izveidotu apakšnodaļas trīsstūri. Skatiet nākamos 10 attēlus, kuriem akordi jāatspoguļo krustojuma darba plaknēs - tie to var izskaidrot labāk nekā tikai vārdi.

7. solis: Doma pabeigšana

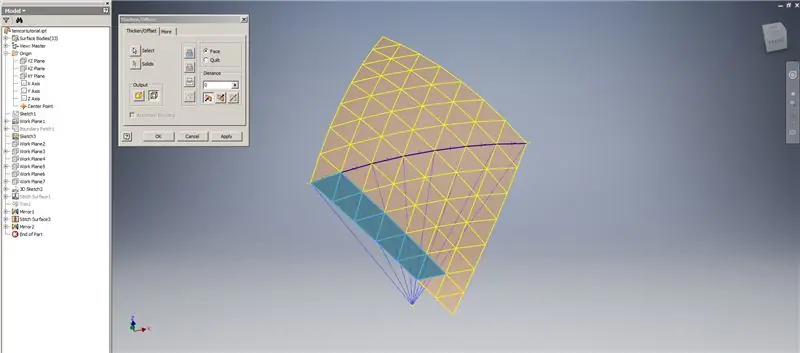
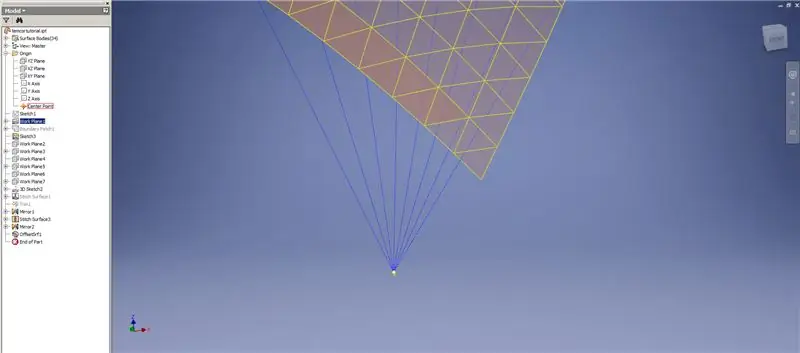
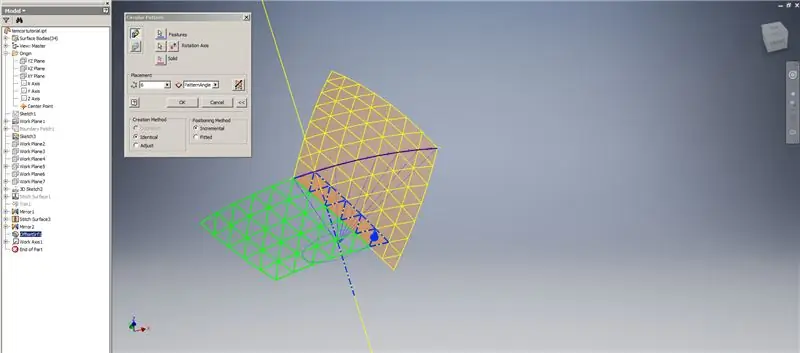
Izveidojiet apakšējo rindu biezumu/nobīdi, izlaižot pēdējās divas trijstūru rindas. Ierakstiet jauno OffsetSrf 6 reizes vai ((Frekvence = 14)/2) -1. Paslēpiet OffsetSrf, sašujiet rakstainas virsmas, pēc tam spoguļojiet sašūto virsmu ar YZ Plane. Izveidojiet darba plaknes, kas balstās uz augšējā trijstūra virsotnēm, kā parādīts 6. attēlā. Izmantojot šīs jaunās darba plaknes, sagrieziet sašūtās un spoguļotās virsmas, pēc tam salieciet atlikušās virsmas kopā. Izveidojiet šo pēdējo virsmu Z asij, pēc tam salieciet šīs pēdējās virsmas kopā, un esat pabeidzis!

8. darbība: akordu pārbaude

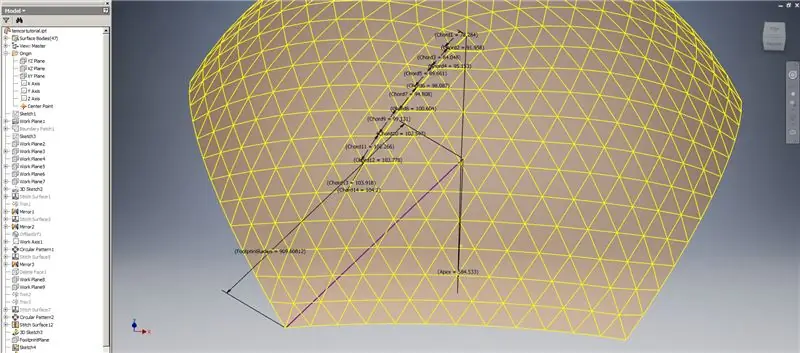
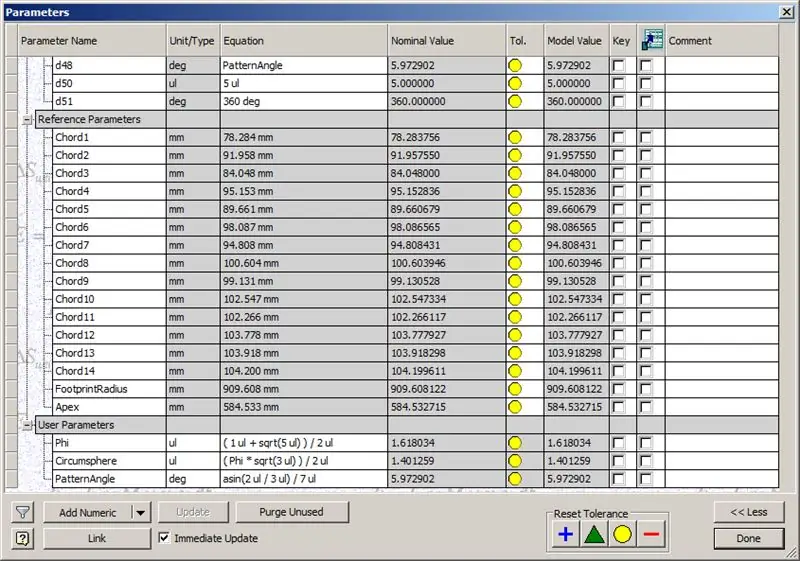
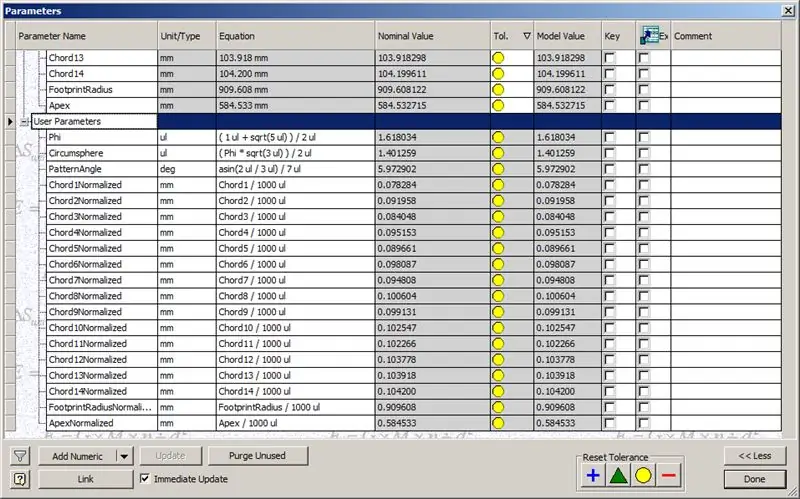
Tātad, mūsu kupols ir pabeigts, bet redzēsim, vai skaitļi atbilst TaffGoch modelim:

Pēc atsauces parametriem izskatās, ka tie ir ideāli saderīgi!

Sadalot akordu garumus ar 1000, mēs skaidri redzam perfektu atbilstību TaffGoch modeļa akordu faktoriem, kā arī pēdas rādiusa un virsotnes faktoriem.